题目内容
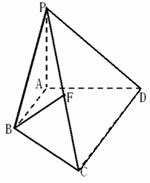
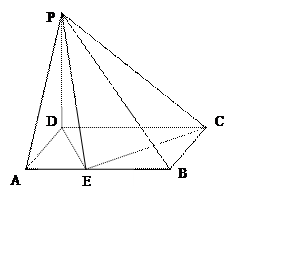
已知:四棱锥P-ABCD,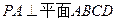 ,底面ABCD是直角梯形,
,底面ABCD是直角梯形, ,且AB∥CD,
,且AB∥CD,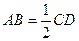 , 点F为线段PC的中点,
, 点F为线段PC的中点,
(1)求证: BF∥平面PAD;
(2) 求证: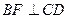 。
。
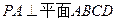 ,底面ABCD是直角梯形,
,底面ABCD是直角梯形, ,且AB∥CD,
,且AB∥CD,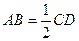 , 点F为线段PC的中点,
, 点F为线段PC的中点, (1)求证: BF∥平面PAD;
(2) 求证:
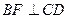 。
。 
证明见解析
(1)证明:取PD的中点E,连结EF、AE,
因为点F为PC的中点,所以EF∥CD,且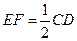 ,
,
而AB∥CD,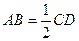 ,所以EF∥AB且EF=AB
,所以EF∥AB且EF=AB
所以四边形EFBA是平行四边形,所以BF∥AE
因为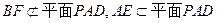
所以BF∥平面PAD (6分)
(2)由题意知 ,
,
又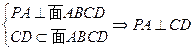 ,
,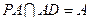 ,
,
所以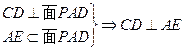
由(1)知BF∥AE
所以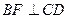
因为点F为PC的中点,所以EF∥CD,且
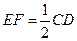 ,
,而AB∥CD,
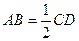 ,所以EF∥AB且EF=AB
,所以EF∥AB且EF=AB所以四边形EFBA是平行四边形,所以BF∥AE
因为
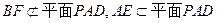
所以BF∥平面PAD (6分)
(2)由题意知
 ,
,又
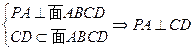 ,
,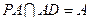 ,
,所以
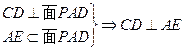
由(1)知BF∥AE
所以

练习册系列答案
相关题目
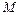 是
是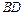 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角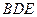 ?若存在,确定点N的位置;
?若存在,确定点N的位置;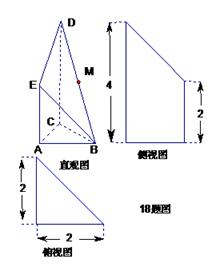
 已知PD=
已知PD=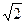 ,CD=2,AE=
,CD=2,AE=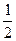 ,
,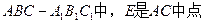 .
.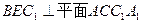 ;
;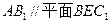 ;
;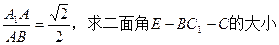 .
.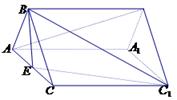
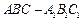 中,
中,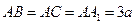 ,
, 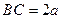 ,
,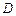 是
是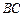 的中点,
的中点,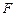 是
是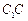 上一点,且
上一点,且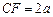 .
.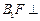 平面
平面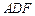 ;
;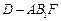 的体积;
的体积;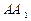 上找一点
上找一点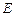 ,使得
,使得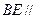 平面
平面
 中,底面
中,底面 是正方形
是正方形
 底面
底面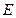 是
是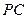 的中点.
的中点.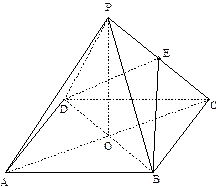
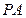 ∥平面
∥平面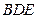 ;
;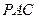
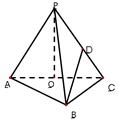
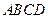 的顶点
的顶点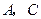 在椭圆
在椭圆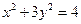 上,对角线
上,对角线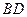 所在直线的斜率为1.
所在直线的斜率为1.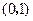 时,求直线
时,求直线 的方程;
的方程;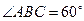 时,求菱形
时,求菱形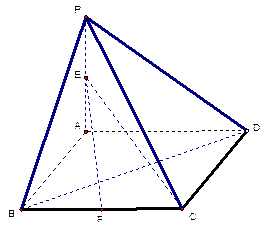
 中,四边形
中,四边形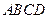 是正方形,
是正方形,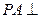 平面
平面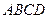 ,
,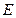 是
是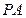 上的一点,
上的一点,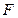 是
是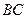 的中点
的中点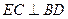 ;
;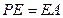 ,求证:
,求证: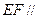 平面
平面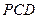 .
.