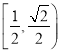题目内容
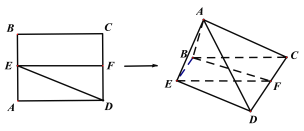
【题目】已知正方形ABCD,E,F分别为AB,CD的中点,将△ADE沿DE折起,使△ACD为等边三角形,如图所示,记二面角A-DE-C的大小为![]() .
.
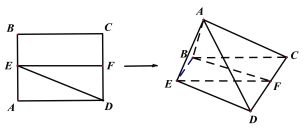
(1)证明:点A在平面BCDE内的射影G在直线EF上;
(2)求角![]() 的正弦值.
的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)过点![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .证明
.证明![]() 在
在![]() 的垂直平分线上,则点
的垂直平分线上,则点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,
上,
(2)以![]() 点为坐标原点,以
点为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 点作平行于
点作平行于![]() 的向量为
的向量为![]() 轴建立空间直角坐标系.设正方形
轴建立空间直角坐标系.设正方形![]() 的边长为
的边长为![]() ,分别求出平面
,分别求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角的余弦值可得角
的一个法向量,由两法向量所成角的余弦值可得角![]() 的正弦值.
的正弦值.
(1)证明:过点A作AG⊥平面BCDE,垂足为G,连接GC,GD.
因为△ACD为等边三角形,所以AC=AD,所以点G在CD的垂直平分线上.
又因为EF是CD的垂直平线,所以点A在平面BCDE内的射影G在直线EF上.
另证:过点A作AG⊥EF,再证AG⊥CD,从而证得AG⊥平面BCDE,
即点A在平面BCDE内的射影G在直线EF上
(2)解:以G为坐标原点,GA所在直线为z轴,GF所在直线为y轴,过点G作平行于DC的直线为x轴建立空间直角坐标系.
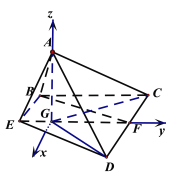
设正方形ABCD的边长为2a,连接AF,
则![]() ,
,![]() ,
,![]()
所以![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则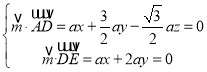 ,
,
令![]() ,得
,得 ,又平面
,又平面![]() 的一个法向量
的一个法向量![]()
所以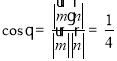 ,
,
![]() .
.

练习册系列答案
相关题目