题目内容
某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛,其得分情况如茎叶图所示:
(1)若从甲运动员的不低于80且不高于90的得分中任选3个,求其中与平均得分之差的绝对值不超过2的概率;
(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值 的分布列与期望.
的分布列与期望.

(1)若从甲运动员的不低于80且不高于90的得分中任选3个,求其中与平均得分之差的绝对值不超过2的概率;
(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值
 的分布列与期望.
的分布列与期望.
(1)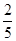 ;(2)
;(2) 的分布列为:
的分布列为:
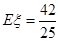 .
.
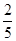 ;(2)
;(2) 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 5 | 6 |
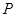 | 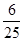 | 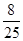 |  | 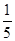 | 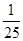 | 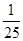 |
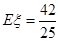 .
.试题分析:(1)由题设要求,根据茎叶图写出甲的所有成绩,计算出平均成绩,然后计数不低于80且不高于90的得分有5个,其中与平均分的差的绝对值不超过2的有4个,那么就可以很快计算出所要要求的概率;(2)从图中可知符合要求的成绩甲、乙各有5个,各取一个其差的绝对值可能为
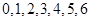 ,我们只要根据
,我们只要根据 的各种情形,列出甲、乙的成绩可能性,可一一求出相应的概率,列出其分布列,再根据公式求出其数学期望.
的各种情形,列出甲、乙的成绩可能性,可一一求出相应的概率,列出其分布列,再根据公式求出其数学期望.(1)由茎叶图可知,甲运动员七轮比赛的得分情况为:78,81,84,85,84,85,91.
所以甲每轮比赛的平均得分为
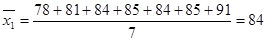
甲运动员每轮比赛得分中不低于80且不高于90的得分共有5个,
分别为81,84,85,84,85,其中81分与平均得分的绝对值大于2,
所求概率
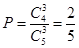 4分
4分(2)设甲、乙两名运动员的得分分别为
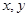 ,则得分之差的绝对值为
,则得分之差的绝对值为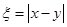 .
.由茎叶图可知,
 的可能取值为0,1,2,3,5,6.
的可能取值为0,1,2,3,5,6.当
 =0时,
=0时,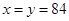 ,故
,故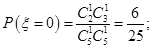
当
 =1时,
=1时,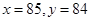 或
或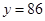 ,故
,故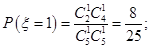
当
 =2时,
=2时,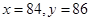 或
或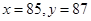 ,故
,故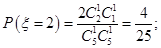
当
 =3时,
=3时,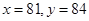 或
或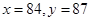 ,故
,故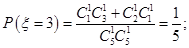
当
 =5时,
=5时,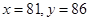 ,故
,故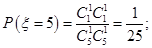
当
 =6时,
=6时,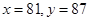 ,故
,故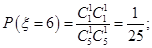 所以
所以 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 5 | 6 |
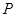 | 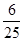 | 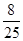 |  | 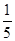 | 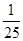 | 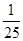 |
 --12分
--12分
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

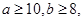 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.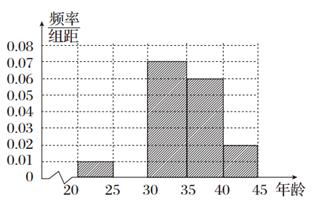
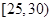 ,第2组
,第2组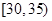 ,第3组
,第3组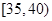 ,第4组
,第4组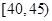 ,第5组
,第5组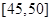 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。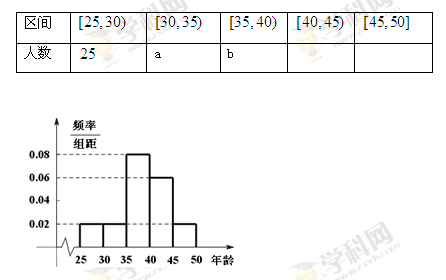
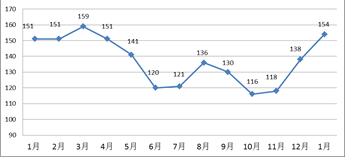
 本月价格指数
本月价格指数 上月价格指数.规定:当
上月价格指数.规定:当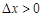 时,称本月价格指数环比增长;
时,称本月价格指数环比增长;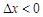 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当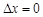 时,称本月价格指数环比持平.
时,称本月价格指数环比持平. 组
组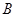 组
组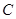 组
组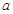
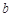
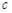
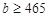 ,
,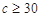 ,求通过测试的概率.
,求通过测试的概率.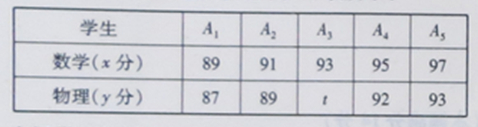
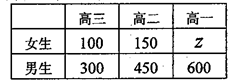
 ,那么表中t的值为 .
,那么表中t的值为 .