题目内容
已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002, ,800进行编号;
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)

(2)抽取的100的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42,若在该样本中,数学成绩优秀率是30%,求a,b的值:
(3)在地理成绩及格的学生中,已知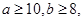 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)

(2)抽取的100的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42,若在该样本中,数学成绩优秀率是30%,求a,b的值:
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
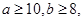 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.(1)785,667,199(2) (3)
(3)
 (3)
(3)
试题分析:
(1)考查的是随机数表法,所以从第8行第7列的第一个开始数三个数构成一个三位数,该三位数必须小于或等于800,如果大于800,则舍去,继续数直到得到三个小于或等于800的三位数,即为最先检查的3个人的编号.
(2)根据数学成绩的优秀率和总人数100可以列出关于a,b的两个方程进而求出a,b的值.
(3)由总人数为100可以得到关于a+b=31,则可以得到a可以取的值和c可以取的值(两者相互确定),进而得到所有的基本事件,在所有基本事件中找出满足a<b的基本事件数,再根据古典概型的概率计算公式即可求出相应的概率.
试题解析:
(1)依题意,最先检测的3个人的编号依次为785,667,199; 3分
(2)由
 ,得
,得 , 5分
, 5分∵
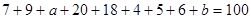 ,
,∴
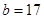 ; 7分
; 7分(3)由题意,知
 ,且
,且 ,
,∴满足条件的
 有:(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),(16,15),
有:(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),(16,15),(17,14),(18,13),(19,12),(20,11),(21,10),(22,9),(23,8)共14组,
且每组出现的可能性相同. 9分
其中数学成绩为优秀的人数比及格的人数少有:
(10,21),(11,20),(12,19),(13,18),(14,17),(15,16)共6组. 11分
∴数学成绩为优秀的人数比及格的人数少的概率为
 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
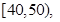
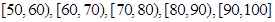 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 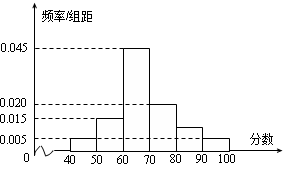
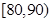 的频率;
的频率;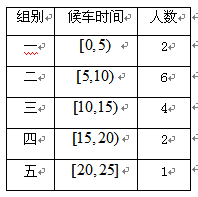
 ,第二类在
,第二类在 ,第三类在
,第三类在 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 
 为获奖户数,求
为获奖户数,求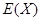 与方差
与方差 .
. 的分布列与期望.
的分布列与期望.