题目内容
为研究学生物理成绩与数学成绩是否相关,某中学老师将一次考试中五名学生的数学、物理成绩记录如下表所示:
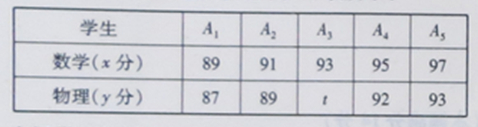
根据上表提供的数据,经检验物理成绩与数学成绩呈线性相关,且得到y关于x的线性回归方程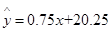 ,那么表中t的值为 .
,那么表中t的值为 .

根据上表提供的数据,经检验物理成绩与数学成绩呈线性相关,且得到y关于x的线性回归方程
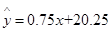 ,那么表中t的值为 .
,那么表中t的值为 .89
试题分析:因为
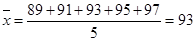 ,把点
,把点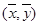 代入回归方程为
代入回归方程为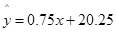 ,得
,得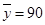 ,
,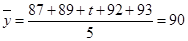 ,解得
,解得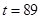 .
.
练习册系列答案
相关题目
题目内容

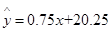 ,那么表中t的值为 .
,那么表中t的值为 .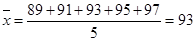 ,把点
,把点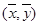 代入回归方程为
代入回归方程为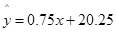 ,得
,得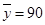 ,
,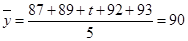 ,解得
,解得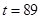 .
.