题目内容
(文科做(1)(2)(4),理科全做)
已知过抛物线C1:y2=2px(p>0)焦点F的直线交抛物线于A(x1,y1),B(x2,y2)两点
(1)证明:y1y2=-p2且(y1+y2)2=2p(x1+x2-p);
(2)点Q为线段AB的中点,求点Q的轨迹方程;
(3)若x1=1,x2=4,以坐标轴为对称轴的椭圆或双曲线C2过A、B两点,求曲线C1和C2的方程;
(4)在(3)的条件下,若曲线C2的两焦点分别为F1、F2,线段AB上有两点C(x3,y3),D(x4,y4)(x3<x4),满足:①S△F1F2A-S△F1F2C=S△F1F2D-S△F1F2B,②AB=3CD.在线段F1 F2上是否存在一点P,使PD=
,若存在,求出点P的坐标;若不存在,说明理由.
已知过抛物线C1:y2=2px(p>0)焦点F的直线交抛物线于A(x1,y1),B(x2,y2)两点
(1)证明:y1y2=-p2且(y1+y2)2=2p(x1+x2-p);
(2)点Q为线段AB的中点,求点Q的轨迹方程;
(3)若x1=1,x2=4,以坐标轴为对称轴的椭圆或双曲线C2过A、B两点,求曲线C1和C2的方程;
(4)在(3)的条件下,若曲线C2的两焦点分别为F1、F2,线段AB上有两点C(x3,y3),D(x4,y4)(x3<x4),满足:①S△F1F2A-S△F1F2C=S△F1F2D-S△F1F2B,②AB=3CD.在线段F1 F2上是否存在一点P,使PD=
| 11 |
分析:(1)设AB:x=my+
,代入y2=2px,利用根与系数的关系即可得出;
(2)设线段AB的中点坐标为M(x,y),则x1+x2=2x,y1+y2=2y.再利用(1)的结论即可得出.
(3)利用(1)的距离即可得到p,即抛物线的方程,进而得到点A,B的坐标.设所求曲线方程为mx2+ny2=1,把点A,B的坐标代入即可得出.
(4)当y1=-2
时,由①②可得
即可解得x4,可得点D的坐标,设P(0,t)由c2=
(c为曲线C2的半焦距),可知,-
≤t≤
,由|PD|=
求得t.当y1=-2
时,同理可得.
| p |
| 2 |
(2)设线段AB的中点坐标为M(x,y),则x1+x2=2x,y1+y2=2y.再利用(1)的结论即可得出.
(3)利用(1)的距离即可得到p,即抛物线的方程,进而得到点A,B的坐标.设所求曲线方程为mx2+ny2=1,把点A,B的坐标代入即可得出.
(4)当y1=-2
| 2 |
|
| 52 |
| 5 |
|
|
| 11 |
| 2 |
解答:解:(1)设AB:x=my+
,代入y2=2px得: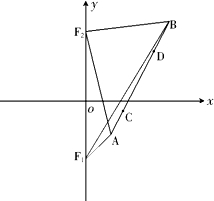
y2-2pmy-p2=0,
∴y1y2=-p2,
∵2p(x1+x2-p)=2px1+2px2-2p2=y12+y22-2p2=(y1+y2)2-2y1y2-2p2
=(y1+y2)2+2p2-2p2=(y1+y2)2
∴(y1+y2)2=2p(x1+x2-p).
(2)设线段AB的中点坐标为M(x,y),则x1+x2=2x,y1+y2=2y
∴4y2=2p(2x-p)
即中点的轨迹方程为y2=px-
p2.
(3)由(1)可得,x1x2=
=4,∴p=4 曲线 C1:y2=8x
∴A(1,-2
),B(4,4
)或A(1,2
),B(4,-4
)
设所求曲线方程为mx2+ny2=1,则
解得
∴曲线C2:
y2-
x2=1.
(4)由(3)可知:y1=±2
①当y1=-2
时,由①②可得
解得
此时D(3,2
),
设P(0,t)由c2=
(c为曲线C2的半焦距),
可知,-
≤t≤
,
由PD=
求得t1=
,t2=3
(舍去)
∴存在点P(0,
)
②当y1=2
时,同理解出点P(0,-
).
| p |
| 2 |

y2-2pmy-p2=0,
∴y1y2=-p2,
∵2p(x1+x2-p)=2px1+2px2-2p2=y12+y22-2p2=(y1+y2)2-2y1y2-2p2
=(y1+y2)2+2p2-2p2=(y1+y2)2
∴(y1+y2)2=2p(x1+x2-p).
(2)设线段AB的中点坐标为M(x,y),则x1+x2=2x,y1+y2=2y
∴4y2=2p(2x-p)
即中点的轨迹方程为y2=px-
| 1 |
| 2 |
(3)由(1)可得,x1x2=
| p2 |
| 4 |
∴A(1,-2
| 2 |
| 2 |
| 2 |
| 2 |
设所求曲线方程为mx2+ny2=1,则
|
|
∴曲线C2:
| 5 |
| 32 |
| 1 |
| 4 |
(4)由(3)可知:y1=±2
| 2 |
①当y1=-2
| 2 |
|
|
此时D(3,2
| 2 |
设P(0,t)由c2=
| 52 |
| 5 |
可知,-
|
|
由PD=
| 11 |
| 2 |
| 2 |
∴存在点P(0,
| 2 |
②当y1=2
| 2 |
| 2 |
点评:熟练掌握圆锥曲线的标准方程及其性质、直线与圆锥曲线相交问题转化为方程联立得到根与系数的关系、中点的坐标公式、三角形的面积计算公式、分类讨论的思想方法等是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 是函数
是函数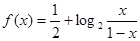 图象上任意两点,且
图象上任意两点,且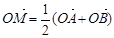 ,已知点
,已知点 的横坐标为
的横坐标为 ,且有
,且有 ,其中
,其中 且n≥2,
且n≥2, ,
, ,
, 及
及 ;
;  ,其中
,其中 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切