题目内容
求下列不等式的解集:
(1)6x2-x-1≥0
(2)(文科选做)-x2+4x+5<0
(3)(理科选做)
≥2.
(1)6x2-x-1≥0
(2)(文科选做)-x2+4x+5<0
(3)(理科选做)
| x | x2-8x+15 |
分析:(1)先解方程6x2-x-1=0,再根据函数图象可知图象在x轴上或x轴上方上的点的横坐标满足题意,从而得出原不等式6x2-x-1≥0的解;
(2)先解方程-x2+4x+5=0的两解为x1=5,x2=-1,根据函数图象可知原不等式-x2+4x+5<0的解;
(3)原不等式通过移项通分等价于
≤0.利用根轴法即可得到原不等式的解集.
(2)先解方程-x2+4x+5=0的两解为x1=5,x2=-1,根据函数图象可知原不等式-x2+4x+5<0的解;
(3)原不等式通过移项通分等价于
| (x-6)(2x-5) |
| (x-3)(x-5) |
解答: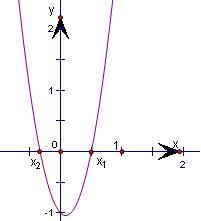 解:(1)方程6x2-x-1=0的两解为x1=
解:(1)方程6x2-x-1=0的两解为x1=
,x2=-
,
根据函数图象可知,
原不等式6x2-x-1≥0的解为{x|x≥
或x≤-
}…(7分)
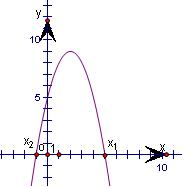
(2)(文科选做)方程-x2+4x+5=0的两解为x1=5,x2=-1,
根据函数图象可知原不等式-x2+4x+5<0的解为{x|x<-1或x>5}…(14分)
(3)(理科选做)原不等式等价于:
-2≥0?
≥0?
≤0
?
≤0?
≤x<3或5<x≤6.

∴原不等式的解集为[
,3)∪(5,6]…(14分)
 解:(1)方程6x2-x-1=0的两解为x1=
解:(1)方程6x2-x-1=0的两解为x1=| 1 |
| 2 |
| 1 |
| 3 |
根据函数图象可知,
原不等式6x2-x-1≥0的解为{x|x≥
| 1 |
| 2 |
| 1 |
| 3 |
(2)(文科选做)方程-x2+4x+5=0的两解为x1=5,x2=-1,
根据函数图象可知原不等式-x2+4x+5<0的解为{x|x<-1或x>5}…(14分)
(3)(理科选做)原不等式等价于:
| x |
| x2-8x+15 |
| -2x2+17x-30 |
| x2-8x+15 |
| 2x2-17x+30 |
| x2-8x+15 |
?
| (x-6)(2x-5) |
| (x-3)(x-5) |
| 5 |
| 2 |


∴原不等式的解集为[
| 5 |
| 2 |
点评:此题考查了一元二次不等式的解法、其他不等式的解法.利用了转化的思想,其中转化的理论依据为两数相乘,同号得正、异号得负的取符号法则.灵活运用化归法是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目