题目内容
已知φ(x)=
,a为正常数.(e=2.71828…);
(理科做)(1)若f(x)=lnx+φ(x),且a=
,求函数f(x)在区间[1,e]上的最大值与最小值
(2)若g(x)=|lnx|+φ(x),且对任意x1,x2∈(0,2],x1≠x2都有
<-1,求a的取值范围.
(文科做)(1)当a=2时描绘?(x)的简图
(2)若f(x)=?(x)+
,求函数f(x)在区间[1,e]上的最大值与最小值.
| a |
| x+1 |
(理科做)(1)若f(x)=lnx+φ(x),且a=
| 9 |
| 2 |
(2)若g(x)=|lnx|+φ(x),且对任意x1,x2∈(0,2],x1≠x2都有
| g(x2)-g(x1) |
| x2-x1 |
(文科做)(1)当a=2时描绘?(x)的简图
(2)若f(x)=?(x)+
| 1 |
| ?(x) |
分析:(理科)(1)本小题需要先求出函数f(x)=lnx+
的导函数f′(x)=
-
=
,然后得出单调区间,利用单调性来求出函数的最大和最小值,属于基本题目;
(2)本题函数g(x)=|lnx|+φ(x)含有绝对值号,考虑到去掉绝对值较为繁琐,也不可行,因此采用整体上处理,即构造一个新的函数来结合单调性求解,由已知
<-1,可以变形为
<0,因此构造函数ω(x)=g(x)+x,
即ω(x)=|lnx|+x+
,(a>0,x∈(0,2]),然后求解.
(文科)(1)本题的函数图象简图的作法可以利用图象变换来做,考查函数φ(x)=
与函数y=
的图象之间的关系来作出;
(2)由已知求得函数的导函数,利用单调性求出函数的最大(小)值来方法同(理科)(1)类似..
| 9 |
| 2(x+1) |
| 1 |
| x |
| 9 |
| 2(x+1)2 |
| 2x2-5x+2 |
| 2x(x+1)2 |
(2)本题函数g(x)=|lnx|+φ(x)含有绝对值号,考虑到去掉绝对值较为繁琐,也不可行,因此采用整体上处理,即构造一个新的函数来结合单调性求解,由已知
| g(x2)-g(x1) |
| x2-x1 |
| g(x2)+x2-[g(x1)+x1] |
| x2-x1 |
即ω(x)=|lnx|+x+
| a |
| x+1 |
(文科)(1)本题的函数图象简图的作法可以利用图象变换来做,考查函数φ(x)=
| 2 |
| x+1 |
| 2 |
| x |
(2)由已知求得函数的导函数,利用单调性求出函数的最大(小)值来方法同(理科)(1)类似..
解答:解:(理科)(1)∵f(x)=lnx+
(x>0)
∴f′(x)=
-
=
(2分)
故当
<x<2时,f'(x)<0,即f(x)单调递减,从而x∈[1,2)时,f(x)单调递减,
当0<x≤
或x≥2时,f'(x)≥0,即f(x)单调递增,从而x∈[2,e]时,f(x)单调递增,(4分)
故fmin(x)=f(2)=ln2+
,又f(1)=
>f(e)=1+
,故fmax=f(1)=
(2)由
<-1可知
<0
所以可设ω(x)=g(x)+x=|lnx|+x+
(a>0,x∈(0,2])…(8分)
故由题设可知ω(x)在x∈(0,2]上为减函数,
∵ω′=
…(10分)
而 由
+1-
<0(1≤x≤2)可得a>x2+3x+3+
(1≤x≤2)
而y=x2+3x+3+
在x∈[1,2]上是增函数,
∴a>
.
显然当a>
且0<x<1时,-
+1-
<0
a=
时,也成立,
所以a的取值范围是[
,+∞)…(14分)
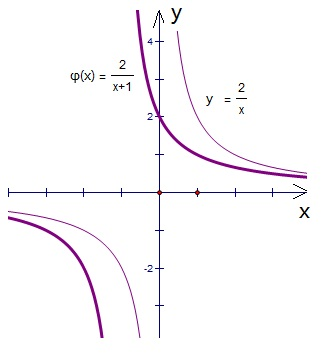
(文科)(1)由已知φ(x)=
,其图象是由反比例函数图象y=
的图象向左平行移动1个单位长度所得到,如图:
(2)由已知f(x)=
+
(a>0),于是有f′(x)=
+
=
,显然f′(x)>0在[1,e]上恒成立,所以函数f(x)在区间[1,e]上为增函数,
所以fmax=f(e)=
+
,fmin=f(1)=
+
| 9 |
| 2(x+1) |
∴f′(x)=
| 1 |
| x |
| 9 |
| 2(x+1)2 |
| 2x2-5x+2 |
| 2x(x+1)2 |
故当
| 1 |
| 2 |
当0<x≤
| 1 |
| 2 |
故fmin(x)=f(2)=ln2+
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2(e+1) |
| 9 |
| 4 |
(2)由
| g(x2)-g(x1) |
| x2-x1 |
| g(x2)+x2-[g(x1)+x1] |
| x2-x1 |
所以可设ω(x)=g(x)+x=|lnx|+x+
| a |
| x+1 |
故由题设可知ω(x)在x∈(0,2]上为减函数,
∵ω′=
|
而 由
| 1 |
| x |
| a |
| (x+1)2 |
| 1 |
| x |
而y=x2+3x+3+
| 1 |
| x |
∴a>
| 27 |
| 2 |
显然当a>
| 27 |
| 2 |
| 1 |
| x |
| a |
| (x+1)2 |
a=
| 27 |
| 2 |
所以a的取值范围是[
| 27 |
| 2 |
(文科)(1)由已知φ(x)=
| 2 |
| x+1 |
| 2 |
| x |

(2)由已知f(x)=
| a |
| x+1 |
| x+1 |
| a |
| a |
| (x+1)2 |
| 1 |
| a |
| a2+(x+1)2 |
| a(x+1)2 |
所以fmax=f(e)=
| a |
| e+1 |
| e+1 |
| a |
| a |
| 2 |
| 2 |
| a |
点评:本题考查了函数的导数及其应用,利用导数求最大(小)值,利用导数以及结合给定的函数的单调区间求解参数的范围,另外考查了函数的图象的画法,综合考查了数形结合思想,分类思想,函数与方程的思想,构造函数解决问题的思想.

练习册系列答案
相关题目