Question

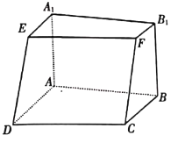
【题目】如图，在正三棱柱（侧棱垂直于底面，且底面三角形是等边三角形）中，，分别是的中点.

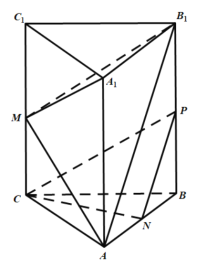
（1）求证：平面∥平面；

（2）在线段上是否存在一点使平面？若存在，确定点的位置；若不存在，也请说明理由.

Answer 1

【答案】（1）证明见解析；（2）存在；点在处

【解析】

（1）要证明平面∥平面，只需证明∥平面，∥平面即可；

（2）在线段上存在一点，它就是点，连接，过点作垂直于，垂足为，连接，只需证明，，再利用线面垂直的判定定理即可得到证明.

证明：（1）因为分别是的中点，

所以∥，

又因为平面，平面，所以∥平面.

因为分别是的中点，四边形为平行四边形，

所以，且∥，

所以四边形是平行四边形，

所以∥.

又因为平面，平面，

所以∥平面.

又因为，平面，平面，

所以平面∥平面.

（2）在线段上存在一点，它就是点，使得平面.

连接，过点作垂直于，垂足为，连接.

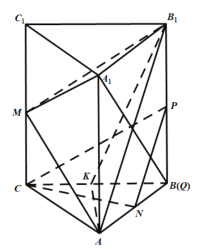
因为在正三棱柱中，，底面三角形是等边三角形，

所以四边形是正方形，

所以.

易证，

所以，

所以，

所以，

因为，三棱柱为直三棱柱，

所以平面.

又因为平面，

所以.

又因为，平面，平面，

所以平面.

又因为平面，所以.

又，平面，平面，

所以平面.