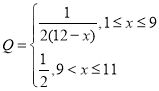题目内容
【题目】洛萨![]() 科拉茨
科拉茨![]() Collatz,
Collatz,![]() 是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半
是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半![]() 即
即![]() ;如果n是奇数,则将它乘3加
;如果n是奇数,则将它乘3加![]() 即
即![]() ,不断重复这样的运算,经过有限步后,一定可以得到
,不断重复这样的运算,经过有限步后,一定可以得到![]() 如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,
如初始正整数为6,按照上述变换规则,我们得到一个数列:6,3,10,5,16,8,4,2,![]() 对科拉茨
对科拉茨![]()
![]() 猜想,目前谁也不能证明,更不能否定
猜想,目前谁也不能证明,更不能否定![]() 现在请你研究:如果对正整数
现在请你研究:如果对正整数![]() 首项
首项![]() 按照上述规则施行变换
按照上述规则施行变换![]() 注:1可以多次出现
注:1可以多次出现![]() 后的第八项为1,则n的所有可能的取值为______.
后的第八项为1,则n的所有可能的取值为______.
【答案】![]()
【解析】
从第八项为![]() 出发,按照规则,逆向逐项推导,即可求出
出发,按照规则,逆向逐项推导,即可求出![]() 的所有可能的取值。
的所有可能的取值。
如果正整数![]() 按照上述规则施行变换后的第
按照上述规则施行变换后的第![]() 项为
项为![]() ,
,
则变换中的第![]() 项一定是
项一定是![]() ;变换中的第
;变换中的第![]() 项一定是
项一定是![]() ;
;
变换中的第![]() 项可能是
项可能是![]() ,也可能是
,也可能是![]() ;
;
当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;
;
当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() 或
或![]()
当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() 或
或![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;
;
当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() 或
或![]() ;当第
;当第![]() 项是
项是![]() 时,变换中的第
时,变换中的第![]() 项是
项是![]() 或
或![]()
则![]() 的所有可能的取值为
的所有可能的取值为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
本题正确结果为:![]()

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
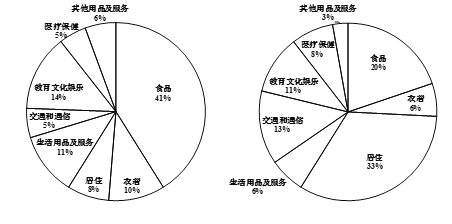
小学教材完全解读系列答案【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于![]() 的同学中任选
的同学中任选![]() 人,求选到的
人,求选到的![]() 人身高都在
人身高都在![]() 以下的概率
以下的概率
(Ⅱ)从该小组同学中任选![]() 人,求选到的
人,求选到的![]() 人的身高都在
人的身高都在![]() 以上且体重指标都在
以上且体重指标都在![]() 中的概率.
中的概率.
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表:
列联表:
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)判断能否有![]() 的把握认为是否生二孩与头胎的男女情况有关;附:
的把握认为是否生二孩与头胎的男女情况有关;附:
| 0,15 | 0.05 | 0.01 | 0.0012.0 |
k | 2.072 | 3.841 | 6.635 | 10.828 |
 (其中
(其中![]() ).
).