题目内容
如果一个水平放置的图形的斜二测直观图是一个底面角为45°，腰和上底均为1的等腰梯形，求原来图形的面积．分析：原图为直角梯形，上底为1，高为2，下底为1+
，利用梯形面积公式求解即可．也可利用原图和直观图的面积关系求解．
| 2 |
解答：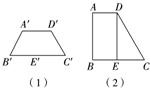
解：恢复后的原图形为一直角梯形，如图（2），
其上底为1，高为2，下底为1+
，
面积S=
（1+
+1）×2=2+
．
故选原来图形的面积为：2+
．
解：恢复后的原图形为一直角梯形，如图（2），其上底为1，高为2，下底为1+
| 2 |
面积S=
| 1 |
| 2 |
| 2 |
| 2 |
故选原来图形的面积为：2+
| 2 |
点评：本题考查水平放置的平面图形的直观图斜二测画法，属基础知识的考查．
练习册系列答案
相关题目
如果一个水平放置的图形的斜二测直观图是一个底面为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是（ ）A、2+
| ||||
B、
| ||||
C、
| ||||
D、1+
|
如图，如果一个水平放置的图形的斜二测直观图是一个等腰直角三角形，斜边长为1，那么原平面图形的面积是（ ）