题目内容
在空间直角坐标系中,已知O (0,0,0) ,A(2,-1,3),B(2,1,1).
(1)求|AB|的长度;
(2)写出A、B两点经此程序框图执行运算后的对应点A0,B0的坐标,并求出 在
在 方向上的投影.
方向上的投影.
(1) ;(2)
;(2) =(2,-1,3),
=(2,-1,3), =(2,1,3);
=(2,1,3);
解析试题分析:(1)有空间两点间的距离可得AB两点的距离.本小题关键是考查空间中两点的距离公式,本公式类似平面中两点的距离公式.
(2)由程序框图可知对空间坐标中的z要求符合一个不等式.通过循环结构即可求得符合要求的z的值.根据向量在另一向量的投影即为该向量的模长与这两向量夹角的余弦值的乘积.本小题通过向量知识与立几知识的交汇,难度不大.有新意.
试题解析:在空间直角坐标系中,已知O (0,0,0) ,A(2,-1,3),B(2,1,1).
(1)
(2)∵A(2,-1,3)满足 22+(-1)2≤32
∴输出A0(2,-1,3)
∵B(2,1,1)不满足22+12≤12
∴z=z+1=2
∵(2,1,2)不满足22+12≤22
∴z=z+1=3
∵(2,1,3)满足22+12≤32
∴输出B0(2,1,3)
∴ =(2,-1,3),
=(2,-1,3), =(2,1,3)
=(2,1,3)
∴
∴ 在
在 方向上的投影等于
方向上的投影等于 

考点:1.空间中两点的距离.2.程序框图.3.空间中的直线关系.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知 (
( ),计算得
),计算得 ,
, ,
, ,
, ,
, ,由此推算:当
,由此推算:当 时,有( )
时,有( )
A. ( ( ) ) |
B. ( ( ) ) |
C. ( ( ) ) |
D. ( ( ) ) |
把正整数按一定的规则排成了如图所示的三角形数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左往右数第
行,从左往右数第 个数,若
个数,若 ,则
,则 与
与 的和为( )
的和为( )
| A.105 | B.103 | C.82 | D.81 |
用数学归纳法证明“ 时,从“
时,从“ 到
到 ”时,左边应增添的式子是( )
”时,左边应增添的式子是( )
A. | B. | C. | D. |
若a,b∈R,则下面四个式子中恒成立的是( )
| A.lg(1+a2)>0 | B.a2+b2≥2(a-b-1) |
| C.a2+3ab>2b2 | D. < <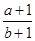 |
 ,
, ,若
,若 的运算规则如右图的程序框图所示,则
的运算规则如右图的程序框图所示,则 的值是____________
的值是____________
 和S=
和S= ,求数列{an}的通项公式.
,求数列{an}的通项公式.
 的值是
的值是 ,则输出
,则输出 的值是
的值是 
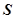 的值为
的值为 