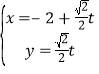题目内容
【题目】过点![]() 斜率为正的直线交椭圆
斜率为正的直线交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.![]() ,
,![]() 是椭圆上相异的两点,满足
是椭圆上相异的两点,满足![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() .则
.则![]() 外接圆半径的最小值为( )
外接圆半径的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
分析可知,P,C,D在一个阿波罗尼斯圆上,设其半径为r,且![]() ,分直线AB斜率存在及不存在两种情况分别讨论得解.
,分直线AB斜率存在及不存在两种情况分别讨论得解.
如图,
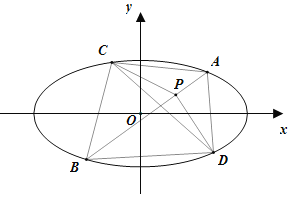
先固定直线AB,设![]() ,则
,则![]() ,其中
,其中![]() 为定值,
为定值,
故点P,C,D在一个阿波罗尼斯圆上,且![]() 外接圆就是这个阿波罗尼斯圆,设其半径为r,阿波罗尼斯圆会把点A,B其一包含进去,这取决于BP与AP谁更大,不妨先考虑
外接圆就是这个阿波罗尼斯圆,设其半径为r,阿波罗尼斯圆会把点A,B其一包含进去,这取决于BP与AP谁更大,不妨先考虑![]() 的阿波罗尼斯圆的情况,BA的延长线与圆交于点Q,PQ即为该圆的直径,如图:
的阿波罗尼斯圆的情况,BA的延长线与圆交于点Q,PQ即为该圆的直径,如图:
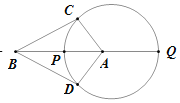
接下来寻求半径的表达式,
由![]() ,解得
,解得![]() ,
,
同理,当![]() 时有,
时有,![]() ,
,
综上,![]() ;
;
当直线AB无斜率时,与椭圆交点纵坐标为![]() ,则
,则![]() ;
;
当直线AB斜率存在时,设直线AB的方程为![]() ,即
,即![]() ,
,
与椭圆方程联立可得![]() ,
,
设![]() ,
,![]() ,则由根与系数的关系有,
,则由根与系数的关系有,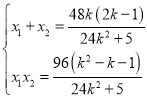 ,
,
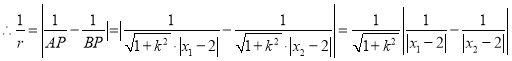 ,
,
注意到![]() 与
与![]() 异号,故
异号,故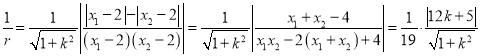 ,
,
设![]() ,则
,则 ,,当
,,当![]() ,即
,即![]() ,此时
,此时![]() ,故
,故![]() ,
,
又![]() ,综上外接圆半径的最小值为
,综上外接圆半径的最小值为![]() .
.
故选:D.

 阅读快车系列答案
阅读快车系列答案【题目】迈入2018年后,直播答题突然就火了.在1月6号的一场活动中,最终仅有23人平分100万,这23人可以说是“学霸”级的大神.随着直播答题的发展,平台“烧钱大战”模式的可持续性受到了质疑,某网站随机选取1000名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 360 | 280 |
认为直播答题模式不可持续 | 240 | 120 |
(1)根据表格中的数据,能否在犯错误不超过![]() 的前提下,认为对直播答题模式的态度与性别有关系?
的前提下,认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的1000人中,有20%曾参加答题游戏瓜分过奖金,而男性被调查者有15%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式: ![]() .
.
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |