题目内容
【题目】如图,边长为![]() 的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=
的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=![]() AB=1,点M在线段EC上.
AB=1,点M在线段EC上.
(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为![]() .
. 
【答案】证明:(Ⅰ)∵DC=BC=1,DC⊥BC,
∴BD=![]() ,
,
∵AD=![]() ,AB=2,
,AB=2,
∴AD2+BD2=AB2 ,
∴∠ADB=90°,
∴AD⊥BD,
∵平面ADEF⊥平面ABCD,ED⊥AD,平面ADEF∩平面ABCD=AD,
∴ED⊥平面ABCD,
∴BD⊥ED,
∵AD∩DE=D,
∴BD⊥平面ADEF,
∵BD平面BDM,
∴平面BDM⊥平面ADEF;
(Ⅱ)解:如图,在平面DMC内,过M作MN⊥DC,垂足为N,则MN∥ED,
∵ED⊥平面ABCD,
∴MN⊥平面ABCD,
∵VB﹣CDM=VM﹣CDB=![]() ,
,
∴![]() X
X![]() X1X1XMN=
X1X1XMN=![]() ,
,
∴MN=![]() ,
,
∴![]() =
=![]() ,
,
∴CM=![]() CE,
CE,
∴点M在线段CE的三等分点且靠近C处.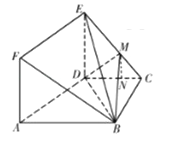
【解析】(Ⅰ)证明:ED⊥平面ABCD,BD⊥平面ADEF,即可证明平面BDM⊥平面ADEF;
(Ⅱ)在平面DMC内,过M作MN⊥DC,垂足为N,则MN∥ED,利用三棱锥的体积计算公式求出MN,可得结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

