题目内容
【题目】下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1 , F2为焦点,设图示①②③中的双曲线的离心率分别为e1 , e2 , e3、则e1 , e2 , e3的大小关系为( )
A.e1>e2>e3
B.e1<e2<e3
C.e2=e3<e1
D.e1=e3>e2
【答案】D
【解析】解:①设等边三角形的边长为2,以底边为x轴,以底边的垂直平分线为y轴,建立平面直角坐标系,
则双曲线的焦点为(±1,0),且过点(![]() ,
, ![]() ),
),
∵(![]() ,
, ![]() )到两个焦点(﹣1,0),(1,0)的距离分别是
)到两个焦点(﹣1,0),(1,0)的距离分别是![]()
∴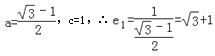
②正方形的边长为![]() , 分别以两条对角线为x轴和y轴,建立平面直角坐标系,
, 分别以两条对角线为x轴和y轴,建立平面直角坐标系,
则双曲线的焦点坐标为(﹣1,0)和(1,0),且过点(![]() ,
,![]() ).
).
∵点(![]() ,
,![]() )到两个焦点(﹣1,0),(1,0)的距离分别是
)到两个焦点(﹣1,0),(1,0)的距离分别是![]()
∴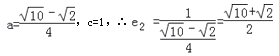
③设正六边形的边长为2,以F1F1所在直线为x轴,以F1F1的垂直平分线为y轴,建立平面直角坐标系,
则双曲线的焦点为(﹣2,0)和(2,0),且过点(1,![]() ),
),
∵点(1,![]() )到两个焦点(﹣2,0)和(2,0)的距离分别为2
)到两个焦点(﹣2,0)和(2,0)的距离分别为2![]() 和2,
和2,
∴a=![]() ﹣1,c=2,∴
﹣1,c=2,∴![]() .
.
所以e1=e3>e2 . 故选D.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目

