题目内容
3．不等式|x+1|+|x-2|≤|2x-1|的解集为{x|x≤-1，或 x≥2}．分析 把要解的不等式等价转化为与之等价的四个不等式组，求出每个不等式组的解集，再取并集，即得所求．
解答 解：由不等式|x+1|+|x-2|≤|2x-1|，可得 $\left\{\begin{array}{l}{x＜-1}\\{-x-1+2-x≤1-2x}\end{array}\right.$ ①，或$\left\{\begin{array}{l}{-1≤x＜\frac{1}{2}}\\{x+1+2-x≤1-2x}\end{array}\right.$ ②，或$\left\{\begin{array}{l}{\frac{1}{2}≤x＜2}\\{x+1+2-x≤2x-1}\end{array}\right.$ ③，或$\left\{\begin{array}{l}{x≥2}\\{x+1+x-2≤2x-1}\end{array}\right.$④．
解①求得x＜-1，解②求得x=-1，解③求得x∈∅，解④求得x≥2．
综上可得，不等式的解集为{x|x≤-1，或 x≥2}，
故答案为：{x|x≤-1，或 x≥2}．
点评 本题主要考查绝对值不等式的解法，关键是去掉绝对值，化为与之等价的不等式组来解，属于基础题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
4．为了考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校的高中生中随机地抽取了300名学生进行调查，得到如下列联表：
由表中数据计算K2≈4.513，判断高中生的性别与是否喜欢数学课程之间是否有关系，并说明理由．
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
14．定积分：$\int_{-\frac{π}{2}}^{\frac{π}{2}}{（{x+sinx}）}dx$=（ ）
| A． | $\frac{π^2}{8}+1$ | B． | $\frac{π^2}{4}+2$ | C． | 1 | D． | 0 |
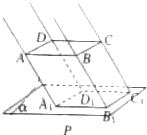如图所示，平面四边形ABCD所在的平面与平面α平行，且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边，则四边形ABCD的形状一定是平行四边形．