题目内容
1.设函数f′(x)是奇函数f(x)的导函数,f(1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1).分析 由已知当x>0时总有xf′(x)-f(x)<0成立,可判断函数g(x)=$\frac{f(x)}{x}$为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(-∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,模拟g(x)的图象,而不等式f(x)>0等价于x•g(x)>0,数形结合解不等式组即可得到答案.
解答 解:令g(x)=$\frac{f(x)}{x}$,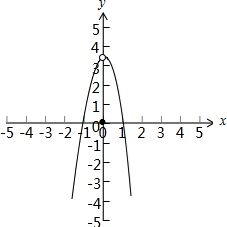
则$g′(x)=\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵xf′(x)-f(x)<0,
∴g′(x)<0,
∴g(x)在(0,+∞)上为减函数,
又∵g(-x)=$\frac{f(-x)}{-x}=\frac{-f(x)}{-x}=\frac{f(x)}{x}$=g(x),
∴函数g(x)为定义域上的偶函数.
又∵g(1)=$\frac{f(1)}{1}$=0,
∴函数g(x)的图象的大致形状如图:
不等式f(x)>0?x•g(x)>0,
由图可知:$\left\{\begin{array}{l}{x>0}\\{g(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{g(x)<0}\end{array}\right.$,
解得:0<x<1或x<-1,
∴f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1),
故答案为:(-∞,-1)∪(0,1).
点评 本题主要考查了利用导数判断函数的单调性,并由函数的奇偶性和单调性解不等式,由题意构造函数g(x)=$\frac{f(x)}{x}$是解答该题的关键,属中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
16.在△ABC中,有a=2b,且C=30°,则这个三角形一定是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |