题目内容
20.在直三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,AA′=$\sqrt{3}$a,则直线AB′与侧面AC′所成角的正切值为$\frac{\sqrt{39}}{13}$.分析 取A'C'的中点D,连接B'D,AD,由线面垂直的性质和判定定理,得到B'D⊥平面AC',则∠B'AD即为直线AB′与侧面AC′所成的角,再由解直角三角形的知识,即可得到所成角的正切值.
解答 解:取A'C'的中点D,连接B'D,AD,
则由底面边长为a的正三角形,得,B'D=$\frac{\sqrt{3}}{2}$a,B'D⊥A'C',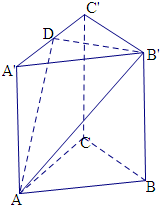
在直三棱柱中,AA'⊥底面A'B'C',
则AA'⊥B'D,即有B'D⊥平面AC',
则∠B'AD即为直线AB′与侧面AC′所成的角,
在直角三角形B'AD中,B'D=$\frac{\sqrt{3}}{2}$a,AD=$\frac{\sqrt{13}}{2}$a,
则tan∠B'AD=$\frac{\sqrt{39}}{13}$.
故直线AB′与侧面AC′所成角的正切值为$\frac{\sqrt{39}}{13}$.
故答案为:$\frac{\sqrt{39}}{13}$.
点评 本题考查线面垂直的判定和性质定理及运用,考查空间直线与平面所成的角的求法,考查运算能力,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
5. 如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题中,错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题中,错误的是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题中,错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题中,错误的是( )| A. | 点H是△A1BD的垂心 | B. | 直线AH与CD1的成角为900 | ||
| C. | AH的延长线经过点C1 | D. | 直线AH与BB1的成角为450 |
 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,点E,F,G分别为PB,PA,BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,点E,F,G分别为PB,PA,BC的中点.