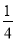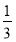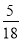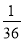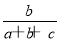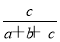题目内容
设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．
(1)当a＝3，b＝2，c＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2球所得分数之和，求ξ的分布列；
(2)从该袋子中任取(每球取到的机会均等)1个球，记随机变量η为取出此球所得分数．若E(η)＝
，D(η)＝
，求a∶b∶c.
（1）ξ的分布列为
ξ | 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
（2）3∶2∶1
【解析】(1)由题意得ξ＝2,3,4,5,6.
故P(ξ＝2)＝
，
P(ξ＝3)＝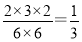
，
P(ξ＝4)＝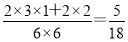
，
P(ξ＝5)＝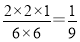
，
P(ξ＝6)＝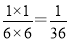
.
所以ξ的分布列为
ξ | 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
(2)由题意知η的分布列为
η | 1 | 2 | 3 |
P |
|
|
|
所以E(η)＝
＋
＋
＝
，
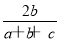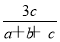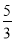D(η)＝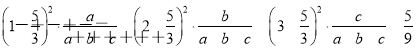
.
化简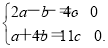得
解得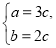
故a∶b∶c＝3∶2∶1.
练习册系列答案
相关题目
已知x与y之间的几组数据如下表：
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得线性回归直线方程
＝
x＋
，若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y＝b′x＋a′，则以下结论正确的是( )．
A.
>b′，
>a′ B.
>b′，
<a′
C.
<b′，
>a′ D.
<b′，
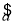<a′
