Question

【题目】某市房管局为了了解该市市民年月至年月期间买二手房情况，首先随机抽样其中名购房者，并对其购房面积（单位：平方米，）进行了一次调查统计，制成了如图所示的频率分布直方图，接着调查了该市年月至年月期间当月在售二手房均价（单位：万元/平方米），制成了如图所示的散点图（图中月份代码分别对应年月至年月）.

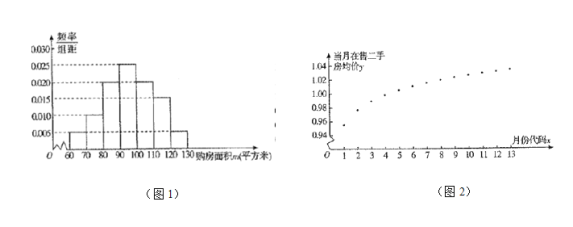
（1）试估计该市市民的购房面积的中位数；

（2）现采用分层抽样的方法从购房面积位于的位市民中随机抽取人，再从这人中随机抽取人，求这人的购房面积恰好有一人在的概率；

（3）根据散点图选择和两个模型进行拟合，经过数据处理得到两个回归方程，分别为和，并得到一些统计量的值如下表所示：

	0.000591	0.000164
	0.006050

请利用相关指数判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测出年月份的二手房购房均价（精确到）

（参考数据），，，，，，

（参考公式）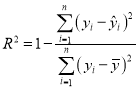

Answer 1

【答案】(1) ； (2) (3) 模型的拟合效果更好；万元/平方米

【解析】

（1）先由频率分布直方图，求出前三组频率和与前四组频率和，确定中位数出现在第四组，根据中位数两侧的频率之和均为，即可得出结果；

（2）设从位于的市民中抽取人，从位于的市民中抽取人，根据分层抽样，求出，；由列举法确定从人中随机抽取人所包含的基本事件个数，以及满足条件的基本事件个数，进而可求出概率；

（3）根据题中数据，分别求出两种模型对应的相关指数，比较大小，即可确定拟合效果；再由确定的模型求出预测值即可.

（1）由频率分布直方图，可得，前三组频率和为，

前四组频率和为，

故中位数出现在第四组，且.

（2）设从位于的市民中抽取人，从位于的市民中抽取人，

由分层抽样可知：，则，

在抽取的人中，记名位于的市民为，，，位于的市民为则所有抽样情况为：，，，，，共6种.

而其中恰有一人在口的情况共有种，故所求概率

（3）设模型和的相关指数分别为，，

则，显然

故模型的拟合效果更好.

由年月份对应的代码为，

则万元/平方米