题目内容
(本小题10分)设等比数列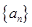 的各项均为正值,首项
的各项均为正值,首项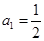 ,前n项和为
,前n项和为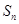 ,且
,且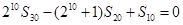
(1)求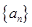 的通项;(2)求
的通项;(2)求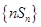 的前n项和
的前n项和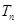
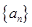 的各项均为正值,首项
的各项均为正值,首项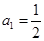 ,前n项和为
,前n项和为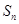 ,且
,且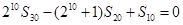
(1)求
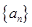 的通项;(2)求
的通项;(2)求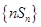 的前n项和
的前n项和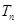
(1)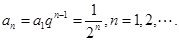 (2)
(2)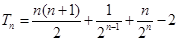 。
。
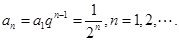 (2)
(2)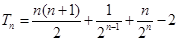 。
。 本试题主要是考查了等比数列的前n项和与通项公式的运用。利用数列的前n项和以及通项公式的表示得到数列的首项和公比的值,得到第一问,然后由于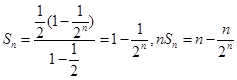 ,则
,则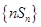 的前n项和
的前n项和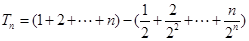 ,利用等差数列和等比数列分组求和,得到结论。
,利用等差数列和等比数列分组求和,得到结论。
(1)由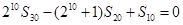 得
得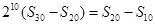
即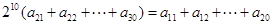
可得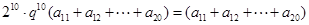 因为
因为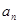 >0,所以
>0,所以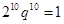
解得 因而
因而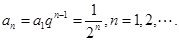
(2)
故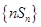 的前n项和
的前n项和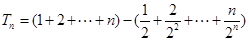
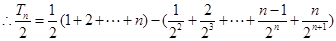
两式相减得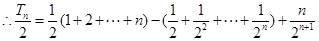
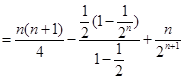
即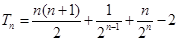
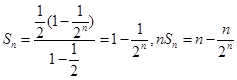 ,则
,则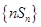 的前n项和
的前n项和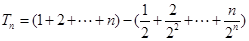 ,利用等差数列和等比数列分组求和,得到结论。
,利用等差数列和等比数列分组求和,得到结论。(1)由
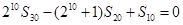 得
得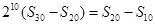
即
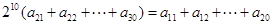
可得
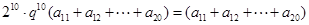 因为
因为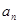 >0,所以
>0,所以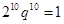
解得
 因而
因而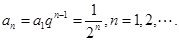
(2)

故
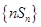 的前n项和
的前n项和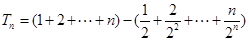
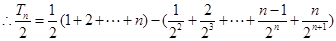
两式相减得
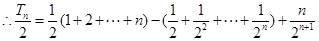
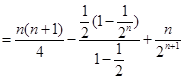
即
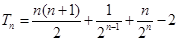

练习册系列答案
相关题目
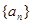 ,其前
,其前 项和为
项和为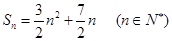 .
.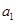 ,
,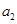 ;
;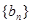 满足
满足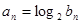 ,请证明数列
,请证明数列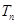 .
.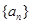 的前
的前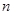 项和为
项和为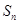 ,且
,且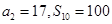 .
.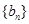 满足
满足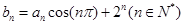 ,求数列
,求数列 ,且
,且 也成等差数列.
也成等差数列.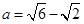 ,求⊿ABC的面积。
,求⊿ABC的面积。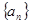 的前
的前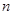 项和为
项和为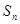 ,等比数列
,等比数列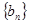 的前
的前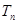 ,它们满足
,它们满足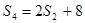 ,
,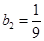 ,
,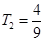 ,且当
,且当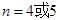 时,
时,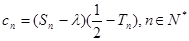 ,如果
,如果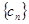 是单调数列,求实数
是单调数列,求实数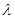 的取值范围.
的取值范围.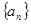 中,
中, ,且满足
,且满足 ,
,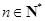 .
.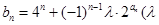 为非零整数,
为非零整数,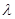 的值,使得对任意
的值,使得对任意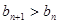 成立.
成立.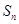 是数列
是数列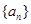 的前
的前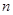 项和,且
项和,且
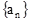 的通项公式;
的通项公式; 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列 (n为正整数),求数列
(n为正整数),求数列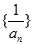 的前
的前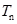 ,若
,若 对
对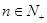 恒成立,求正整数
恒成立,求正整数 的最小值。
的最小值。

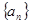 中,公差
中,公差 ,前
,前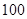 项的和
项的和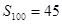 ,
,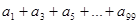 ="_____________."
="_____________."