Question

【题目】已知椭圆C：，（a＞b＞0）过点（1，）且离心率为．

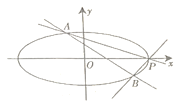
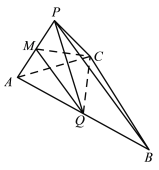
（1）求椭圆C的方程；

（2）设椭圆C的右顶点为P，过定点（2，﹣1）的直线l：y＝kx+m与椭圆C相交于异于点P的A，B两点，若直线PA，PB的斜率分别为k1，k2，求k1+k2的值．

Answer 1

【答案】（1）；（2）1

【解析】

(1)根据题意列出关于满足的关系式再求解即可.

(2)联立直线与椭圆的方程,再设A（x1，y1），B（x2，y2），P（2，0）,进而表达出直线PA，PB的斜率,再利用韦达定理化简求解即可.

（1）由题意可得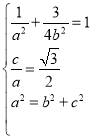，解得a2＝4，b2＝1，

则椭圆的方程为y2＝1，

（2）由题意，过定点（2，﹣1）的直线l：y＝kx+m，

∴﹣1＝2k+m，

∴m＝﹣2k﹣1

A（x1，y1），B（x2，y2），P（2，0）

联立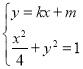得（1+4k2）x2+8kmx+4m2﹣4＝0．

△＝64k2m2﹣4（1+4k2）（4m2﹣4）＝16（4k2﹣m2+1）＞0．

∴x1+x2，x1x2

∵直线PA，PB的斜率分别为k1，k2，

∴k1+k2

kk2k2k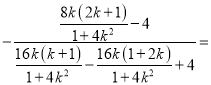2k﹣（2k﹣1）＝1