题目内容
设定义在R上的函数f(x)=a0x4+a1x3+a2x2+a3x+a4,a0,a1,a2,a3,a4∈R,当x=-1时,f(x)取得极大值(1)求f(x)的表达式;
(2)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在[![]() ,
,![]() ]上?如果存在,求出这两点的坐标;如果不存在,请说明理由;
]上?如果存在,求出这两点的坐标;如果不存在,请说明理由;
(3)设xn=![]() ,ym=
,ym=![]() (m,n∈N*),求证:|f(xn)-f(ym)|<
(m,n∈N*),求证:|f(xn)-f(ym)|<![]() .
.
解:(1)将y=f(x+1)的图象向右平移1个单位,得到y=f(x)的图象,
所以y=f(x)的图象关于点(0,0)对称,即y=f(x)是奇函数.
所以f(x)=a1x3+a3x.由题意,得
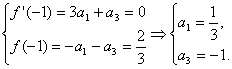
所以f(x)=![]() x3-x.
x3-x.
(2)由(1)得f′(x)=x2-1,
假设存在两切点为(x1,f(x1)),(x2,f(x2))(x1,x2∈[![]() ,
,![]() ]),
]),
则f′(x1)·f′(x2)=(x12-1)(x22-1)=-1.
因为(x12-1)、(x22-1)∈[-1,1],
所以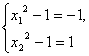 或
或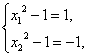 即
即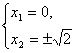 或
或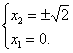
从而可得所求两点的坐标分别为(0,0),(![]() ,
,![]() )或(0,0),(-
)或(0,0),(-![]() ,
,![]() ).
).
(3)证明:因为当x∈[![]() ,1)时,f′(x)<0,所以f(x)在[
,1)时,f′(x)<0,所以f(x)在[![]() ,1)上单调递减.
,1)上单调递减.
由已知得xn∈[![]() ,1),所以f(xn)∈(f(1),f(
,1),所以f(xn)∈(f(1),f(![]() )],即f(xn)∈(
)],即f(xn)∈(![]() ,
,![]() ].
].
注意到x<-1时,f′(x)>0,-1<x<1时,f′(x)<0,
故f(x)在(-∞,-1)上单调递增,在(-1,1)上单调递减.
由于ym=![]() ,所以ym∈(
,所以ym∈(![]() ,
,![]() ].因为
].因为![]() <-1<
<-1<![]() ,
,
所以f(ym)∈(f(-2),f(-1)],即f(ym)∈(![]() ,
,![]() ],
],
所以|f(xn)-f(ym)|=f(ym)-f(xn)<![]() -(-
-(-![]() )=
)=![]() .
.

练习册系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |