Question

【题目】已知正方体的棱长为2.

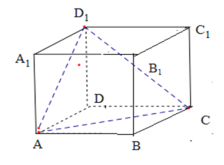
（1）求点到平面的距离；

（2）平面截该正方体的内切球，求截面积的大小；

Answer 1

【答案】（1）；（2）

【解析】

（1）求出平面ACD1的法向量，利用向量法能求出点B到平面ACD1的距离．

（2）根据正方体和球的结构特征，求得球O被平面ACD1所截得的圆的半径即可．

（1）以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，

A（2，0，0），B（2，2，0），C1（0，2，2），C（0，2，0），D1（0，0，2），

（0，﹣2，2），（﹣2，2，0），

（0，2，0），

设平面ACD1的法向量（x，y，z），

则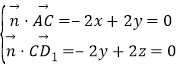，取y＝1，得（1，1，1），

∴点B到平面ACD1的距离d．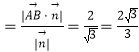

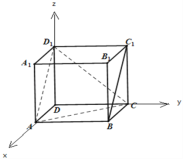
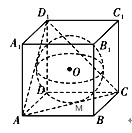
（2）如图，O为球心，也是正方体的中心，

设球O被平面ACD1所截得截面为△AC的内切圆，半径为r，AC中点为M，

则rD1M，

故截面圆的面积π．