题目内容
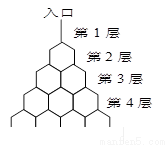
(本题满分12分)如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层,…,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第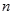 层第
层第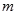 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为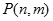 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第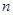 层的第
层的第 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.
(Ⅰ)试求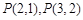 及
及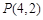 的值,并猜想
的值,并猜想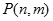 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第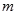 个竖直通道得到分数为
个竖直通道得到分数为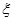 ,其中
,其中 ,试求
,试求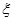 的分布列
的分布列
及数学期望.
【答案】
(1)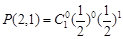 ,
,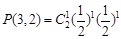
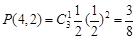
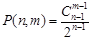 (2)
(2)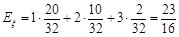
【解析】
试题分析:(Ⅰ)因为小弹子落入第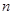 层的第
层的第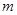 个通道的次数服从二项分布,则:
个通道的次数服从二项分布,则: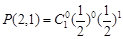 , ……………………………1分
, ……………………………1分
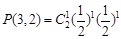 ……………………………3分
……………………………3分
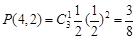 ……………………………4分
……………………………4分
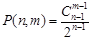 ……………………………6分
……………………………6分
(Ⅱ)依题: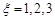 .
.
由(Ⅰ)知,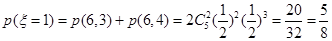
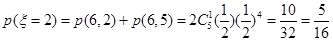
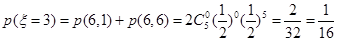 ……………………9分
……………………9分
所以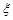 的分布列如下表:
的分布列如下表:
|
|
1 |
2 |
3 |
|
|
|
|
|
……………………11分
故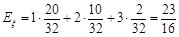 ……………………………12分
……………………………12分
考点:分布列的求解,以及概率的计算
点评:解决该试题的关键是利用古典概型概率公式得到概率值,同时结合分布列的知识求解分布列和数学期望,属于基础题。

练习册系列答案
相关题目
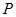
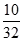
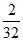
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
