题目内容
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为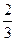 ,被乙小组攻克的概率为
,被乙小组攻克的概率为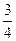 .
.
(1)设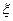 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求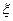 的分布列及
的分布列及 ;
;
(2)设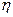 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数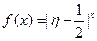 在定义域内单调递增”为事件
在定义域内单调递增”为事件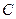 ,求事件
,求事件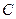 的概率.
的概率.
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为
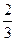 ,被乙小组攻克的概率为
,被乙小组攻克的概率为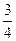 .
.(1)设
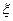 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求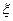 的分布列及
的分布列及 ;
;(2)设
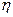 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数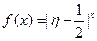 在定义域内单调递增”为事件
在定义域内单调递增”为事件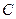 ,求事件
,求事件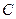 的概率.
的概率.解:记“甲攻关小组获奖”为事件A,则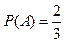 ,记“乙攻关小组获奖”为事件B,则
,记“乙攻关小组获奖”为事件B,则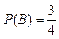 .
.
(I)由题意,ξ的所有可能取值为0,1,2. -------1分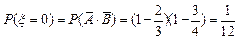 ,
,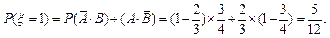
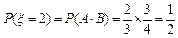 ,
,
∴ξ的分布列为:
----------------5分
∴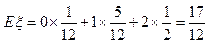 . ---6分
. ---6分
(II)∵获奖攻关小组数的可能取值为0,1,2,相对应没有获奖的攻关小组的取值为2,1,0.
∴η的可能取值为0,4. ------------9分
当η=0时,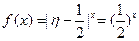 在定义域内是减函数.
在定义域内是减函数.
当η=4时,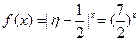 在定义域内是增函数. -------------10分
在定义域内是增函数. -------------10分
∴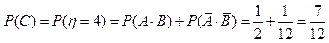 . -----12分
. -----12分
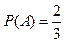 ,记“乙攻关小组获奖”为事件B,则
,记“乙攻关小组获奖”为事件B,则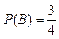 .
.(I)由题意,ξ的所有可能取值为0,1,2. -------1分
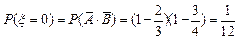 ,
,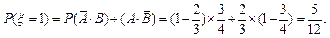
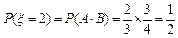 ,
,| ξ | 0 | 1 | 2 |
| P | 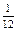 | 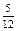 | 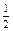 |
----------------5分
∴
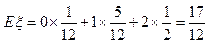 . ---6分
. ---6分(II)∵获奖攻关小组数的可能取值为0,1,2,相对应没有获奖的攻关小组的取值为2,1,0.
∴η的可能取值为0,4. ------------9分
当η=0时,
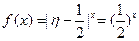 在定义域内是减函数.
在定义域内是减函数.当η=4时,
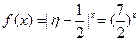 在定义域内是增函数. -------------10分
在定义域内是增函数. -------------10分∴
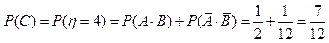 . -----12分
. -----12分略

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
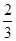 的概率为
的概率为



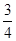 ,若要使存留的污垢不超过原有的
,若要使存留的污垢不超过原有的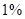 ,
,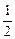 .记小球遇到第
.记小球遇到第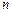 行第
行第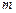 个障碍物(从左至右)上顶点的概率为
个障碍物(从左至右)上顶点的概率为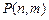 .
.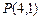 ,
,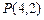 的值,并猜想
的值,并猜想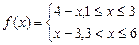 ,设小球遇到第6行第
,设小球遇到第6行第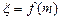 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.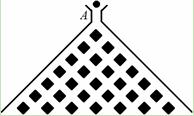


 个人,其中35岁以下抽
个人,其中35岁以下抽 ,求
,求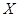 的分布列为
的分布列为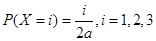 ,则
,则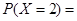 ( )
( )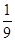
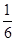
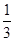
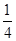
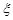 服从正态分布
服从正态分布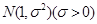 .若
.若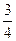 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是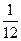 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是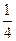 ;
;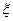 表示回答该题对的人数,求
表示回答该题对的人数,求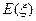 .
.