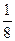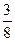题目内容
一条生产线上生产的产品按质量情况分为三类:A类、B类、C类.检验员定时从该生产线上任取2件产品进行一次抽检,若发现其中含有C类产品或2件都是B类产品,就需要调整设备,否则不需要调整.已知该生产线上生产的每件产品为A类品,B类品和C类品的概率分别为0.9,0.05和0.05,且各件产品的质量情况互不影响.
(1)求在一次抽检后,设备不需要调整的概率;
(2)若检验员一天抽检3次,以ξ表示一天中需要调整设备的次数,求ξ的分布列.
(1)求在一次抽检后,设备不需要调整的概率;
(2)若检验员一天抽检3次,以ξ表示一天中需要调整设备的次数,求ξ的分布列.
(1)设Ai表示事件“在一次抽检中抽到的第i件产品为A类品”,
i=1,2.
Bi表示事件“在一次抽检中抽到的第i件产品为B类品”,
i=1,2.
C表示事件“一次抽检后,设备不需要调整”.
则C=A1·A2+A1·B2+B1·A2.
由已知P(Ai)=0.9,P(Bi)=0.05 i=1,2.
所以,所求的概率为
P(C)=P(A1·A2)+P(A1·B2)+P(B1·A2)
=0.92+2×0.9×0.05=0.9.
(2)由(1)知一次抽检后,设备需要调整的概率为
p=P()=1-0.9=0.1,依题意知ξ~B(3,0.1),ξ的分布列为
i=1,2.
Bi表示事件“在一次抽检中抽到的第i件产品为B类品”,
i=1,2.
C表示事件“一次抽检后,设备不需要调整”.
则C=A1·A2+A1·B2+B1·A2.
由已知P(Ai)=0.9,P(Bi)=0.05 i=1,2.
所以,所求的概率为
P(C)=P(A1·A2)+P(A1·B2)+P(B1·A2)
=0.92+2×0.9×0.05=0.9.
(2)由(1)知一次抽检后,设备需要调整的概率为
p=P()=1-0.9=0.1,依题意知ξ~B(3,0.1),ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| p | 0.729 | 0.243 | 0.027 | 0.001 |
略

练习册系列答案
相关题目
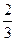 ,被乙小组攻克的概率为
,被乙小组攻克的概率为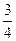 .
.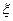 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 ;
;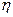 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数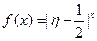 在定义域内单调递增”为事件
在定义域内单调递增”为事件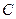 ,求事件
,求事件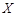 的分布列为
的分布列为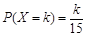 ,
,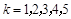 ,则
,则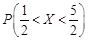 等于( )
等于( )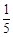
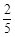
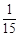
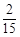
 ,乙击中目标的概率为
,乙击中目标的概率为 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”。
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”。 求一个“单位射击组”为“单位进步组”的概率;
求一个“单位射击组”为“单位进步组”的概率; ,求
,求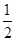
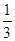
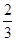
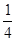
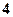 ”的概率为_
”的概率为_