题目内容

【题目】如图，已知圆Q：(x＋2)2＋(y－2)2=1，抛物线C：y2=4x的焦点为F，过F的直线l与抛物线C交于A，B两点，过F且与l垂直的直线l'与圆Q有交点.

（1）求直线l'的斜率的取值范围；

（2）求△AOB面积的取值范围.

【答案】（1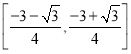）；（2）.

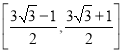【解析】

（1）根据题意设出的方程，由直线与圆有交点，结合圆心到直线的距离小于等于半径即可求得直线的斜率的取值范围；

（2）设，联立抛物线方程，即可得到韦达定理，进而用表示出的距离，由O到AB的距离即可表示，再利用范围求的取值范围

（1）显然，直线l的斜率存在且不为0

设 ，则

由题意可得：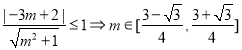

而直线的斜率为所以

所以直线的斜率的取值范围是：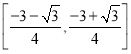

（2）设，联立方程组

化简得：

故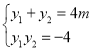

O到直线AB的距离为：

即

所以的面积为

练习册系列答案
相关题目

【题目】已知函数，其中为自然对数的底数．

（1）讨论的单调性；

（2）当时，恒成立，求的取值范围．

【题目】已知函数.

（Ⅰ）讨论函数的单调性；

（Ⅱ）当时，证明：函数有两个零点；

（Ⅲ）若函数有两个不同的极值点，记作，且，证明（为自然对数的底数）.

【题目】为了调节高三学生学习压力，某校高三年级举行了拔河比赛，在赛前三位老师对前三名进行了预测，于是有了以下对话：老师甲：“7班男生比较壮，7班肯定得第一名”．老师乙：“我觉得14班比15班强，14班名次会比15班靠前”．老师丙：“我觉得7班能赢15班”．最后老师丁去观看完了比赛，回来后说：“确实是这三个班得了前三名，且无并列，但是你们三人中只有一人预测准确”．那么，获得一、二、三名的班级依次为( )

A.7班、14班、15班B.14班、7班、15班

C.14班、15班、7班D.15班、14班、7班

【题目】已知抛物线的方程，焦点为，已知点在上，且点到点的距离比它到轴的距离大1.

（1）试求出抛物线的方程；

（2）若抛物线上存在两动点（在对称轴两侧），满足（为坐标原点），过点作直线交于两点，若，线段上是否存在定点，使得恒成立？若存在，请求出的坐标，若不存在，请说明理由.

【题目】如图，椭圆 的左右焦点分别为的、，离心率为；过抛物线焦点的直线交抛物线于、两点，当时， 点在轴上的射影为。连结并延长分别交于、两点，连接； 与的面积分别记为， ，设.

（Ⅰ）求椭圆和抛物线的方程；

（Ⅱ）求的取值范围.

【题目】设函数，，其中恒不为0.

（1）设，求函数在x＝1处的切线方程；

（2）若是函数与的公共极值点，求证：存在且唯一；

（3）设，是否存在实数a，b，使得在(0，)上恒成立？若存在，请求出实数a，b满足的条件；若不存在，请说明理由.

【题目】科赫曲线是一种外形像雪花的几何曲线，一段科赫曲线可以通过下列操作步骤构造得到．任画一条线段，然后把它均分成三等分，以中间一段为边向外作正三角形，并把“中间一段”去掉，这样，原来的条线段就变成了4条小线段构成的折线，称为“一次构造”；用同样的方法把每一条小线段重复上述步骤，得到了16条更小的线段构成的折线，称为“二次构造”，…，如此进行“次构造”，就可以得到一条科曲线．若要科赫曲线的长度达到原来的100倍，至少需要通过构造的次数是（ ）．（取）

A.15B.16C.17D.18

【题目】已知函数，其中为常数.

（1）讨论函数的单调性；

（2）当（为自然对数的底数），时，若方程有两个不等实数根，求实数的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网