题目内容
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中![]() 为实数集,
为实数集,![]() 为有理数集,则关于函数
为有理数集,则关于函数![]() 有如下四个命题:①
有如下四个命题:①![]() ;②函数
;②函数![]() 是偶函数;③任取一个不为零的有理数
是偶函数;③任取一个不为零的有理数![]() ,
,![]() 对任意的
对任意的![]() 恒成立;④存在三个点
恒成立;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中真命题的个数有( )
为等边三角形.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据所给的定义,运用分类讨论的方法、取特殊值法进行逐一判断即可.
①∵当![]() 为有理数时,
为有理数时,![]() ;当
;当![]() 为无理数时,
为无理数时,![]() ,
,
∴当![]() 为有理数时,
为有理数时,![]() ;
;
当![]() 为无理数时,
为无理数时,![]() ,
,
即不管![]() 是有理数还是无理数,均有
是有理数还是无理数,均有![]() ,故①正确;
,故①正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意![]() ,都有
,都有![]() ,故②正确;
,故②正确;
③若![]() 是有理数,则
是有理数,则![]() 也是有理数; 若
也是有理数; 若![]() 是无理数,则
是无理数,则![]() 也是无理数,
也是无理数,
∴根据函数的表达式,任取一个不为零的有理数![]() ,
,![]() 对
对![]() 恒成立,故③正确;
恒成立,故③正确;
④取![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,
∴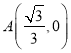 ,
,![]() ,
,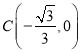 ,恰好
,恰好![]() 为等边三角形,故④正确.
为等边三角形,故④正确.
故选:D.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目