题目内容
【题目】选修4-4:极坐标与参数方程
已知在一个极坐标系中点![]() 的极坐标为
的极坐标为![]() .
.
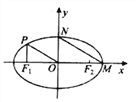
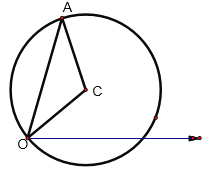
(1)求出以![]() 为圆心,半径长为2的圆的极坐标方程(写出解题过程)并画出图形.
为圆心,半径长为2的圆的极坐标方程(写出解题过程)并画出图形.
(2)在直角坐标系中,以圆![]() 所在极坐标系的极点为原点,极轴为
所在极坐标系的极点为原点,极轴为![]() 轴的正半轴建立直角坐标系,点
轴的正半轴建立直角坐标系,点![]() 是圆
是圆![]() 上任意一点,
上任意一点, ![]() ,
, ![]() 是线段
是线段![]() 的中点,当点
的中点,当点![]() 在圆
在圆![]() 上运动时,求点
上运动时,求点![]() 的轨迹的普通方程.
的轨迹的普通方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)设圆![]() 上任意一点
上任意一点![]()
![]()
![]()
![]()
![]()
![]() 圆
圆![]() 的极坐标方程
的极坐标方程![]() ,作图见解析;(2)设圆
,作图见解析;(2)设圆![]() 上任意一点
上任意一点![]() ,令
,令![]() ,由
,由![]() ,
, ![]() 是线段
是线段![]() 的中点
的中点![]()
![]() 的参数方程为
的参数方程为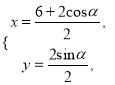
![]()
![]()
点![]() 的轨迹的普通方程为
的轨迹的普通方程为![]() .
.
试题解析: (1)如图,设圆![]() 上任意一点
上任意一点![]() ,则
,则![]() 或
或![]() ,
,
由余弦定理得![]() ,
,
∴圆![]() 的极坐标方程
的极坐标方程![]() ,作图.
,作图.
(2)在直角坐标系中,点![]() 的坐标为
的坐标为![]() ,可设圆
,可设圆![]() 上任意一点
上任意一点![]() ,
,
又令![]() ,由
,由![]() ,
, ![]() 是线段
是线段![]() 的中点,
的中点,
∴![]() 的参数方程为
的参数方程为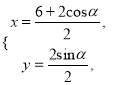 即
即![]() (
(![]() 为参数).
为参数).
∴点![]() 的轨迹的普通方程为
的轨迹的普通方程为![]() .
.

练习册系列答案
相关题目