题目内容
【题目】为了了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验将![]() 只小鼠随机分成
只小鼠随机分成![]() 、
、![]() 两组,每组
两组,每组![]() 只,其中
只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:
组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:


根据频率分布直方图估计,事件![]() :“乙离子残留在体内的百分比不高于
:“乙离子残留在体内的百分比不高于![]() ”发生的概率
”发生的概率![]() .
.
(1)根据所给的频率分布直方图估计各段频数;
(附:频数分布表)
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
(2)请估计甲离子残留百分比的中位数,请估计乙离子残留百分比的平均值.
【答案】(1)见解析;(2)甲离子残留百分比的中位数为![]() ,乙离子残留百分比的平均值为
,乙离子残留百分比的平均值为![]() .
.
【解析】
(1)根据![]() ,求出
,求出![]() 、
、![]() 的值,利用频数、频率和总容量的关系求出每组的频数,填入表格即可;
的值,利用频数、频率和总容量的关系求出每组的频数,填入表格即可;
(2)由甲离子残留百分比直方图中位数左边矩形面积和为![]() 可求出中位数,将每个矩形底边中点值与对应的矩形面积相乘,再将所得结果相加即可得出平均数.
可求出中位数,将每个矩形底边中点值与对应的矩形面积相乘,再将所得结果相加即可得出平均数.
(1)事件![]() :“乙离子残留在体内的百分比不高于
:“乙离子残留在体内的百分比不高于![]() ”发生的概率
”发生的概率![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
因此,频数分布表如下表所示:
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
(2)设甲离子残留百分比的中位数为![]() ,
,
![]() ,
,![]() ,
,
![]() ,解得
,解得![]() .
.
由频率分布直方图可知,乙离子残留百分比的平均值为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】已知直线![]() 所经过的定点
所经过的定点![]() 恰好是椭圆
恰好是椭圆![]() 的一个焦点,且椭圆
的一个焦点,且椭圆![]() 上的点到点
上的点到点![]() 的最大距离为
的最大距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,直线
,直线![]() .试证:当点
.试证:当点![]() 在椭圆
在椭圆![]() 上运动时,直线
上运动时,直线![]() 与圆
与圆![]() 恒相交,并求直线
恒相交,并求直线![]() 被圆
被圆![]() 所截得弦长
所截得弦长![]() 的取值范围.
的取值范围.
【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛,图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
(1)完成下列![]() 的列联表,并回答是否有
的列联表,并回答是否有![]() 的把握认为“两个学段的学生对四大名著的了解有差异”?
的把握认为“两个学段的学生对四大名著的了解有差异”?
成绩小于60分的人数 | 成绩不小于60的人数 | 合计 | |
初中年级 | |||
高中年级 | |||
合计 |
(2)规定竞赛成绩不少于70分的为优秀,按分层抽样的方法从高中,初中年级优秀学生中抽取5人进行复赛,在复赛人员中选3人进行面试,记面试人员中来自初中段的为随机变量X,求随机变量X的分布列与期望.
![]() 其中
其中![]()
附表:
| 0.10 | 0.05 | span>0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6635 | 10.828 |
【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
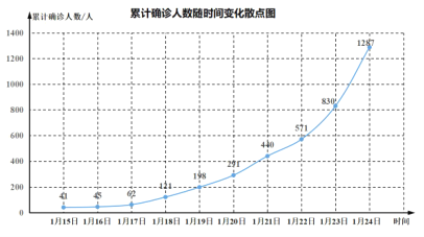
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为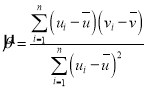 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |