题目内容
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见证明;(2)![]()
【解析】
(1) 设F(x)=e2x+ln(x+1)﹣(x+1)2﹣x(x≥0),通过两次求导,判断F(x)的单调性,即可得证;(2) 由题意可得存在x0∈[0,+∞),使得e![]() ﹣ln(x0+a)﹣x02<0,设
﹣ln(x0+a)﹣x02<0,设![]() =e2x﹣ln(x+a)﹣x2,两次求导,判断单调性,对a讨论,分①当a≥
=e2x﹣ln(x+a)﹣x2,两次求导,判断单调性,对a讨论,分①当a≥![]() 时,②当a<
时,②当a<![]() 时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
(1)设![]() ,
,![]()
F″(x)=4e2x﹣![]() ﹣2=[e2x-
﹣2=[e2x-![]() ]+2(e2x﹣1)+e2x>0,(x≥0),
]+2(e2x﹣1)+e2x>0,(x≥0),
所以,F′(x)在[0,+∞)上递增,所以F′(x)≥F′(0)=0,
所以,F(x)在[0,+∞)上递增,所以F(x)≥F(0)=0,
即有当x≥0时,f(x)≥(x+1)2+x;
(2)即![]() ,
,
则![]() ,
,![]()
![]() 在
在![]() 上递增,
上递增,![]()
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
故![]() ,
,![]()
②当![]() 时,
时,![]()
设![]() ,
,
![]() ,
,
![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
![]() ,
,
![]() ,
,
则当![]() 时,
时,![]() 恒成立,不合题意
恒成立,不合题意
综上,则![]()

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量×(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度(微克/立方米) | 60 | 70 | 74 | 78 | 79 |
(1)根据上表数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)若周六同一时间段的车流量是25万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少(保留整数)?
参考公式:由最小二乘法所得回归直线的方程是:![]() ,其中
,其中 ,
,![]()
【题目】为了了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验将![]() 只小鼠随机分成
只小鼠随机分成![]() 、
、![]() 两组,每组
两组,每组![]() 只,其中
只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:
组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:


根据频率分布直方图估计,事件![]() :“乙离子残留在体内的百分比不高于
:“乙离子残留在体内的百分比不高于![]() ”发生的概率
”发生的概率![]() .
.
(1)根据所给的频率分布直方图估计各段频数;
(附:频数分布表)
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
(2)请估计甲离子残留百分比的中位数,请估计乙离子残留百分比的平均值.
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
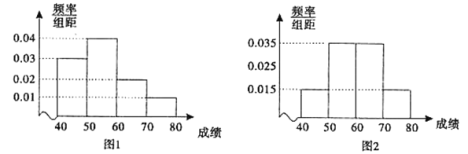
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好

