题目内容
设函数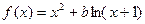 .
.
(1)若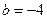 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若函数 在定义域上是单调函数,求
在定义域上是单调函数,求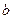 的取值范围;
的取值范围;
(3)若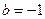 ,证明对任意
,证明对任意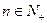 ,不等式
,不等式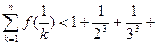 …
… 都成立。
都成立。
解(1)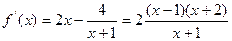 ,定义域
,定义域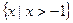
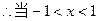 时,
时,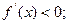 当
当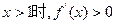 .
.
故函数 的减区间是(-1,1),增区间是(1,+
的减区间是(-1,1),增区间是(1,+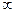 ).
).
(2)∵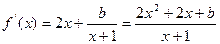 ,又函数
,又函数 在定义域是单调函数,
在定义域是单调函数,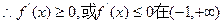 上恒成立。
上恒成立。
若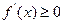 ,
,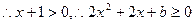 在
在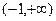 上恒成立,
上恒成立,
即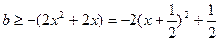 恒成立,由此得
恒成立,由此得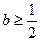 ;
;
若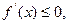 ∵
∵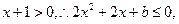 即
即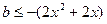 恒成立,
恒成立,
因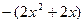 在
在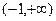 没有最小值,
没有最小值, 不存在实数
不存在实数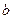 使
使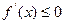 恒成立。
恒成立。
综上所知,实数b的取值范围是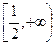 .
.
(3)当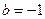 时,函数
时,函数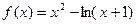 ,令函数
,令函数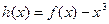
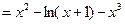 ,
,
则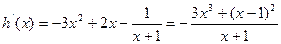 ,
,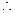 当
当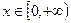 时,
时,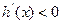 ,
, 函数
函数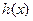 在
在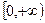 上单调递减,
上单调递减,
又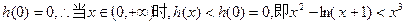 恒成立。
恒成立。
故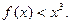 ∵
∵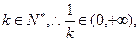 取
取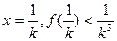 ,
,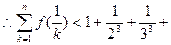 …
… ,故结论成立。
,故结论成立。
解析

练习册系列答案
相关题目
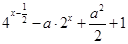 的最大值和最小值.
的最大值和最小值. 

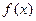 的零点;
的零点;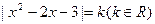 解的情况.
解的情况.
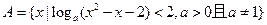 ,
,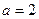 ,求集合
,求集合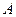 ;
; 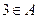 ,求实数
,求实数 的取值范围.
的取值范围. ; ②当
; ②当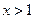 时,
时,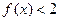 ;
;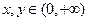 ,总有
,总有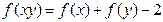
 的值;
的值;
 和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时
和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时 间为
间为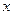 (单位:分),学生的接受能力为
(单位:分),学生的接受能力为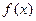 (
(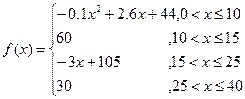
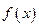 的定义
的定义 域
域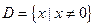 ,且满足对任意
,且满足对任意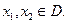
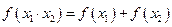
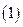 求
求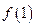 ,
,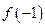 的值。
的值。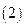 判断
判断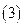 如果
如果 ,
,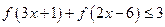 ,且
,且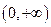 上是增函数,求
上是增函数,求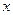 的取值范围。
的取值范围。