题目内容
函数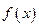 的定义
的定义 域
域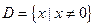 ,且满足对任意
,且满足对任意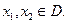
有: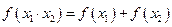
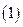 求
求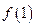 ,
,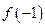 的值。
的值。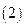 判断
判断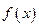 的奇偶性并证明
的奇偶性并证明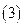 如果
如果 ,
,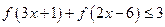 ,且
,且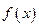 在
在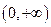 上是增函数,求
上是增函数,求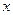 的取值范围。
的取值范围。
解: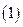 令
令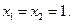 有
有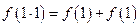 解得:
解得: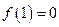
令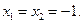 有
有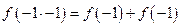 解得:
解得: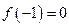 ----3分
----3分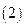
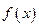 为偶函数,证明如下:
为偶函数,证明如下:
令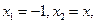 有
有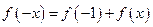 ,
,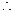
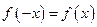 即
即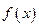 为偶函数。-6分
为偶函数。-6分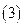
 ,
,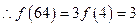
由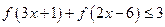 得:
得: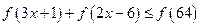
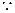
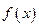 为偶函数,又
为偶函数,又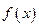 在
在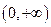 上是增函数
上是增函数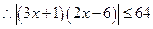 且
且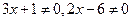 解得:
解得: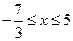 且
且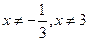
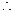
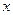 的取值
的取值 范围为{
范围为{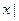
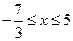 且
且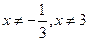 }
}
解析

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
题目内容
函数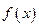 的定义
的定义 域
域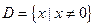 ,且满足对任意
,且满足对任意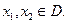
有: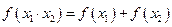
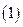 求
求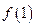 ,
,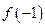 的值。
的值。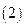 判断
判断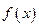 的奇偶性并证明
的奇偶性并证明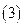 如果
如果 ,
,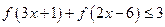 ,且
,且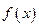 在
在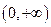 上是增函数,求
上是增函数,求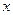 的取值范围。
的取值范围。
解: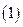 令
令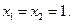 有
有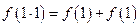 解得:
解得: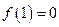
令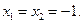 有
有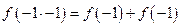 解得:
解得: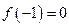 ----3分
----3分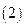
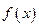 为偶函数,证明如下:
为偶函数,证明如下:
令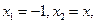 有
有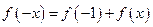 ,
,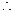
 即
即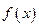 为偶函数。-6分
为偶函数。-6分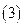
 ,
,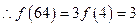
由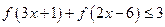 得:
得: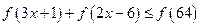
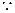
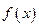 为偶函数,又
为偶函数,又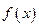 在
在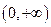 上是增函数
上是增函数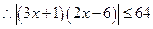 且
且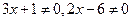 解得:
解得: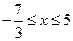 且
且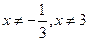
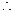
 的取值
的取值 范围为{
范围为{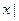
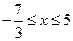 且
且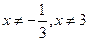 }
}
解析

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案