题目内容
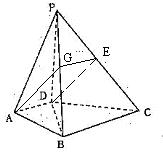
(08年天津南开区质检一理) (12分) 已知如图,在四棱锥P―ABCD中,PD⊥平面ABCD,AD⊥DC,AD//BC,PD:DC:BC=![]() 。
。
(1)证明BC⊥平面PDC;
(2)求二面角D―PB―C的正切值;
(3)若![]() ,求证:平面PAB⊥平面PBC。
,求证:平面PAB⊥平面PBC。

解析:本小题考查直线与直线垂直、直线与平面垂直、平面与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力。
(1)解:由PD⊥平面ABCD,![]() 平面ABCD,得PD⊥BC
平面ABCD,得PD⊥BC
由AD⊥DC,AD//BC,得BC⊥DC
又![]() ,则BC⊥平面PDC(3分)
,则BC⊥平面PDC(3分)
(2)解:取PC中点E,连DE,则DE⊥PC
由BC⊥平面PDC,![]() 平面PBC
平面PBC
得平面PDC⊥平面PBC ∴ DE⊥平面PBC
作EF⊥PB于F,连DF
由三垂线定理,得DF⊥PB
则∠DFE为二面角D―PB―C的平面角
在![]() 中,求得
中,求得![]()
在![]() 中,求得
中,求得![]()
在![]() 中,
中,![]()
即二面角D―PB―C的正切值为![]() (8分)
(8分)
(3)证:取PB中点G,连AG和EG
由三角形中位线定理得GE//BC,![]()
由已知,AD//BC,![]()
∴ AD=GE,AD//GE
则四边形AGED为平行四边形
∴ AG//DE
由(2)已证出DE⊥平面PBC
∴ AG⊥平面PBC
又![]() 平面PAB ∴ 平面PAB⊥平面PBC(12分)
平面PAB ∴ 平面PAB⊥平面PBC(12分)

练习册系列答案
相关题目

