题目内容
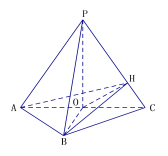
【题目】在![]() 中,
中,![]() 、
、![]() 所对的边长为
所对的边长为![]() 、
、![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)讨论使![]() 有一解、两解、无解时
有一解、两解、无解时![]() 的取值情况.
的取值情况.
【答案】(1)![]() 或
或![]() ;(2)答案不唯一,具体见解析.
;(2)答案不唯一,具体见解析.
【解析】
(1)由正弦定理求得B的正弦值,进而求解;
(2)解法一:固定边![]() (即
(即![]() )和角
)和角![]() ,以
,以![]() 为圆心,边
为圆心,边![]() (即
(即![]() )为半径作圆弧,该圆弧与角
)为半径作圆弧,该圆弧与角![]() 除
除![]() 外的另一边所在射线的交点即为点
外的另一边所在射线的交点即为点![]() .利用几何方法判定解的个数的不同情况的条件;解法二:利用正弦定理求得
.利用几何方法判定解的个数的不同情况的条件;解法二:利用正弦定理求得![]() ,其中
,其中![]() ,转化为函数
,转化为函数![]() 与水平直线
与水平直线![]() 交点的个数,然后利用正弦函数的图象的性质求解.
交点的个数,然后利用正弦函数的图象的性质求解.
(1)由正弦定理,得![]() 或
或![]() ;
;
(2)解法一:
如图所示:
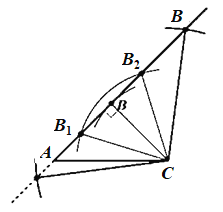
①![]() ,即
,即![]() 时,
时,![]() 无解;
无解;
②![]() 或
或![]() ,即
,即![]() 或
或![]() 时,
时,![]() 有一解;
有一解;
③![]() ,即
,即![]() 时,
时,![]() 有两解.
有两解.
解法二:
应用正弦定理![]() ,得
,得![]() (*),其中
(*),其中![]() ,
,
方程(*)的解![]() 的个数,即函数
的个数,即函数![]() 与水平直线
与水平直线![]() 交点的个数.
交点的个数.
如图所示:
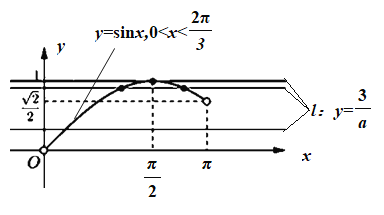
当![]() ,即
,即![]() 时,
时,![]() 无解;
无解;
当![]() 或
或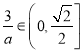 ,即
,即![]() 或
或![]() 时
时![]() 有一解;
有一解;
当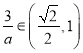 ,即
,即![]() 时
时![]() 有两解;
有两解;

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选手接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: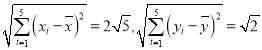
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: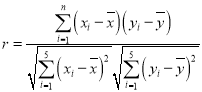 ,
,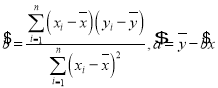
参考数据:![]()