题目内容
【题目】如图,在三棱锥P-ABC中,正三角形PAC所在平面与等腰三角形ABC所在平面互相垂直,AB=BC,O是AC中点,OH⊥PC于H.
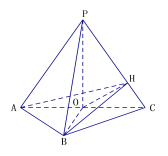
(1)证明:PC⊥平面BOH;
(2)若![]() ,求二面角A-BH-O的余弦值.
,求二面角A-BH-O的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
(1)先证明![]() 平面
平面![]() ,得到
,得到![]() ,结合已知
,结合已知![]() ,证得
,证得![]() 平面
平面![]() .(2)以
.(2)以![]() 为空间坐标原点建立空间直角坐标系,利用平面
为空间坐标原点建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值.
的余弦值.
解:(1)∵AB=BC,O是AC中点,

∴ BO⊥AC,
又平面PAC⊥平面ABC,
且![]() 平面ABC,平面PAC∩平面ABC=AC,
平面ABC,平面PAC∩平面ABC=AC,
∴ BO⊥平面PAC,
∴ BO⊥PC,又OH⊥PC,BO∩OH=O,
∴ PC⊥平面BOH;
(2)易知PO⊥AC,又BO⊥平面PAC,

如图,以O为原点,OB所在的直线为x轴,建立空间直角
坐标系O - xyz,由![]() 易知
易知![]() ,OC=2,
,OC=2,
![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面ABH的法向量为![]() ,
,
则 , ∴
, ∴![]() ,取x=2,得
,取x=2,得![]() ,
,
由(1)知![]() 是平面BHO的法向量,易知
是平面BHO的法向量,易知![]() ,
,
设二面角A-BH-O的大小为![]() ,显然
,显然![]() 为锐角,
为锐角,
则![]()
![]()
![]()
![]() ,
,
∴ 二面角A-BH-O的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为发挥体育在核心素养时代的独特育人价值,越来越多的中学已将某些体育项目纳入到学生的必修课程,甚至关系到是否能拿到毕业证.某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究性学习小组随机从该校高一年级学生中抽取了100人进行调查,其中男生60人,且抽取的男生中对游泳有兴趣的占![]() ,而抽取的女生中有15人表示对游泳没有兴趣.
,而抽取的女生中有15人表示对游泳没有兴趣.
(1)试完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“对游泳是否有兴趣与性别有关”?
的把握认为“对游泳是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)已知在被抽取的女生中有6名高一(1)班的学生,其中3名对游泳有兴趣,现在从这6名学生中随机抽取3人,求至少有2人对游泳有兴趣的概率.
(3)该研究性学习小组在调查中发现,对游泳有兴趣的学生中有部分曾在市级和市级以上游泳比赛中获奖,如下表所示.若从高一(8)班和高一(9)班获奖学生中各随机选取2人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
班级 |
|
|
|
|
|
|
|
|
|
|
|
市级比赛 获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
|
市级以上比赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
|
| 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
【题目】2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | 30 | ||
女生 | 15 | ||
合计 | 120 |
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |

