题目内容
(本小题满分14分)
在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对
称图形),其中矩形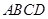 的三边
的三边 、
、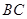 、
、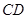 由长6分米的材料弯折而成,
由长6分米的材料弯折而成,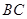 边的长
边的长
为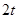 分米(
分米(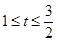 );曲线
);曲线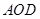 拟从以下两种曲线中选择一种:曲线
拟从以下两种曲线中选择一种:曲线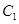 是一段余弦曲线
是一段余弦曲线
(在如图所示的平面直角坐标系中,其解析式为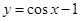 ),此时记门的最高点
),此时记门的最高点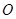 到
到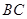
边的距离为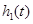 ;曲线
;曲线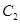 是一段抛物线,其焦点到准线的距离为
是一段抛物线,其焦点到准线的距离为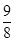 ,此时记门的最高点
,此时记门的最高点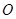
到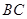 边的距离为
边的距离为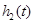 .
.
(1)试分别求出函数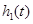 、
、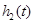 的表达式;
的表达式;
(2)要使得点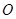 到
到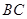 边的距离最大,应选用哪一种曲线?此时,最大值是多少?
边的距离最大,应选用哪一种曲线?此时,最大值是多少?

【答案】
(1)对于曲线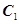 ,因为曲线
,因为曲线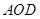 的解析式为
的解析式为 ,所以点D的坐标为
,所以点D的坐标为
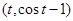 ……2分
……2分
所以点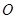 到
到 的距离为
的距离为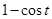 ,而
,而 ,
,
则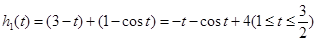 …………4分
…………4分
对于曲线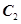 ,因为抛物线的方程为
,因为抛物线的方程为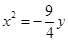 ,即
,即 ,所以点D的坐标为
,所以点D的坐标为
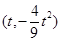 ………2分
………2分
所以点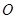 到
到 的距离为
的距离为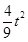 ,
,
而 ,所以
,所以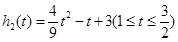 ……………7分
……………7分
(2)因为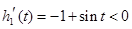 ,所以
,所以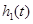 在
在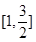 上单调递减,所以当
上单调递减,所以当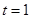 时,
时,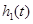 取得
取得
最大值为 ……………………………………………9分
……………………………………………9分
又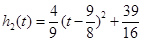 ,而
,而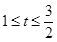 ,
,
所以当 时,
时,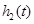 取得最大值为
取得最大值为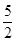 ……………………11分
……………………11分
因为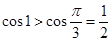 ,所以
,所以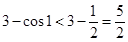 ,
,
故选用曲线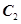 ,当
,当 时,点
时,点 到
到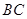 边的距离最大,最大值为
边的距离最大,最大值为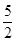 分米…………14分
分米…………14分
【解析】略

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)