题目内容
【题目】求下列函数的定义域:
(1)f(x)=log2![]()
(2)f(x)=![]() .
.
【答案】解:(1)要使函数有意义,则3x﹣2>0,即x>![]() ,
,
即函数的定义域为(![]() ,+∞).
,+∞).
(2)要使函数有意义,则4﹣2x≥0,
即2x≤4,得x≤2,
即函数的定义域为(﹣∞,2].
【解析】根据函数成立的条件即可求出函数的定义域.
【考点精析】认真审题,首先需要了解函数的概念及其构成要素(函数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数),还要掌握函数的定义域及其求法(求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零)的相关知识才是答题的关键.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零)的相关知识才是答题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
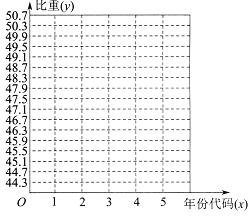
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
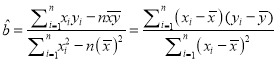 ,
, ![]() .
.