Question

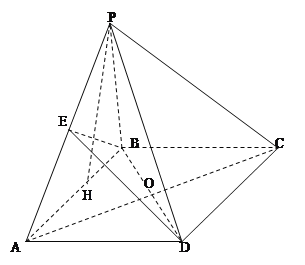
【题目】如图，四棱锥的底面是矩形，平面平面， 是的中点，且， .

（I）求证： 平面；

（II）求三棱锥的体积.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题分析：（I）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往需要利用平几知识，如本题利用三角形中位线得：连接交于点，则（II）求三棱锥的体积，关键在求高，而高一般通过线面垂直得到，本题可以面面垂直性质定理可得线面垂直：利用等腰三角形性质可得（为中点），再利用面面垂直性质定理可得平面.在三角形中求出PH值，及三角形PBD面积，代入体积公式得结果

试题解析：解：（I）连接，交于点，连接，则是的中点.

又∵是的中点，∴是的中位线，∴，

又∵平面， 平面，

∴平面.

（II）取中点，连接，

由得，

又∵平面平面，且平面平面，

∴平面.

∵是边长为2的等边三角形，∴，

又∵，

∴