题目内容
对于定义在D上的函数y=f(x),若同时满足.①存在闭区间[a,b]⊆D,使得任取x1∈[a,b],都有f(x1)=c (c是常数);
②对于D内任意x2,当x2∉[a,b]时总有f(x2)>c称f(x)为“平底型”函数.
(1)(理)判断f1(x)=|x-1|+|x-2|,f2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f1(x)=|x-1|+|x-2|,f2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+
 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值;(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件.
【答案】分析:(1)考查函数是否全部具备“平底型”函数的定义中的2个条件:①在一个闭区间上,函数值是个常数,
②在闭区间外的定义域内,函数值大于此常数.
(2)要使一个式子大于或等于f(x)恒成立,需使式子的最小值大于或等于f(x)即可,从而得到f(x)≤2,
结合“平底型”函数f(x)的图象可得,当x∈[0.5,2.5]时,f(x)≤2成立.
(3)假定函数是“平底型”函数,则函数解析式应满足“平底型”函数的2个条件,
化简函数解析式,检验“平底型”函数的2个条件同时具备的m、n值是否存在.
解答:解:(1)(理)f1(x)是,∵函数定义域R,在区间[1,2]上,f1(x)=1,在区间[1,2]外,f1(x)>1,
f2(x)不是,∵在(-∞,0]上,f2(x)=2,在(-∞,0]外,f2(x)>2,(-∞,0]不是闭区间.
(文)f1(x)是,理由同(理)f1(x),f2(x)不是,∵在[3,+∞)上,f2(x)=3,在[3,+∞)外,f2(x)<3.
(2)(理)|t-k|+|t+k|≥|k|•f(x),即 f(x)≤|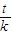 -1|+|
-1|+|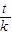 +1|,∵|
+1|,∵|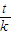 -1|+|
-1|+|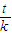 +1|的最小值是2,
+1|的最小值是2,
∴f(x)≤2,又由f(x)=|x-1|+|x-2|,得 x∈[0.5,2.5]时,f(x)≤2,故x的范围是[0.5,2.5].
(文)∵|t-1|+|t+1|≥f(x),|t-1|+|t+1|的最小值是2,∴f(x)≤2,
又由f(x)=|x-1|+|x-2|,得 x∈[0.5,2.5]时,f(x)≤2,故x的范围是[0.5,2.5].
(3)(理)x2+2x+n=(mx-c)2
则m2=1,-2mc=2,c2=n;解得m=1,c=-1,n=1,①,或m=-1,c=1,n=1,②
①情况下,f(x)=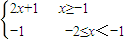 是“平底型”函数;
是“平底型”函数;
②情况下,f(x)=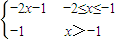 不是“平底型”函数;
不是“平底型”函数;
综上,当m=1,n=1时,为“平底型”函数
(文)f(x)=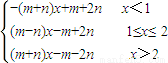
1°当m+n>0时
若m-n=0,是“平底型”函数;若m-n≠0,不是“平底型”函数
2°当m+n<0时,不是“平底型”函数
3°m+n=0
若m-n>0,不是“平底型”函数
若m-n<0,不是“平底型”函数
若m-n=0,f(x)=0,显然不是“平底型”函数.
故当m+n>0,且m-n=0时,是“平底型”函数
点评:本题综合考查函数概念及构成要素,及不等式中的恒成立问题,体现等价转化和分类讨论的数学思想.
②在闭区间外的定义域内,函数值大于此常数.
(2)要使一个式子大于或等于f(x)恒成立,需使式子的最小值大于或等于f(x)即可,从而得到f(x)≤2,
结合“平底型”函数f(x)的图象可得,当x∈[0.5,2.5]时,f(x)≤2成立.
(3)假定函数是“平底型”函数,则函数解析式应满足“平底型”函数的2个条件,
化简函数解析式,检验“平底型”函数的2个条件同时具备的m、n值是否存在.
解答:解:(1)(理)f1(x)是,∵函数定义域R,在区间[1,2]上,f1(x)=1,在区间[1,2]外,f1(x)>1,
f2(x)不是,∵在(-∞,0]上,f2(x)=2,在(-∞,0]外,f2(x)>2,(-∞,0]不是闭区间.
(文)f1(x)是,理由同(理)f1(x),f2(x)不是,∵在[3,+∞)上,f2(x)=3,在[3,+∞)外,f2(x)<3.
(2)(理)|t-k|+|t+k|≥|k|•f(x),即 f(x)≤|
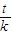 -1|+|
-1|+|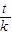 +1|,∵|
+1|,∵|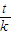 -1|+|
-1|+|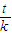 +1|的最小值是2,
+1|的最小值是2,∴f(x)≤2,又由f(x)=|x-1|+|x-2|,得 x∈[0.5,2.5]时,f(x)≤2,故x的范围是[0.5,2.5].
(文)∵|t-1|+|t+1|≥f(x),|t-1|+|t+1|的最小值是2,∴f(x)≤2,
又由f(x)=|x-1|+|x-2|,得 x∈[0.5,2.5]时,f(x)≤2,故x的范围是[0.5,2.5].
(3)(理)x2+2x+n=(mx-c)2
则m2=1,-2mc=2,c2=n;解得m=1,c=-1,n=1,①,或m=-1,c=1,n=1,②
①情况下,f(x)=
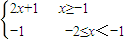 是“平底型”函数;
是“平底型”函数;②情况下,f(x)=
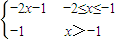 不是“平底型”函数;
不是“平底型”函数;综上,当m=1,n=1时,为“平底型”函数
(文)f(x)=
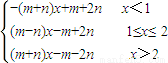
1°当m+n>0时
若m-n=0,是“平底型”函数;若m-n≠0,不是“平底型”函数
2°当m+n<0时,不是“平底型”函数
3°m+n=0
若m-n>0,不是“平底型”函数
若m-n<0,不是“平底型”函数
若m-n=0,f(x)=0,显然不是“平底型”函数.
故当m+n>0,且m-n=0时,是“平底型”函数
点评:本题综合考查函数概念及构成要素,及不等式中的恒成立问题,体现等价转化和分类讨论的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目