在平面直角坐标系中.设向量$\overrightarrow{a}$=(1.2).$\overrightarrow{b}$=.则$\overrightarrow{a}$．($\overrightarrow{a}$-$\overrightarrow{b}$)=4．题目和参考答案——青夏教育精英家教网—

题目内容

1．在平面直角坐标系中，设向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），则$\overrightarrow{a}$．（$\overrightarrow{a}$-$\overrightarrow{b}$）=4．

分析根据向量的坐标运算和数量积运算直接求出即可．

解答解：由题意得，向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），
则$\overrightarrow{a}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）=（1，2）•（4，0）=4，
故答案为：4．

点评本题考查向量的坐标运算和数量积运算，属于基础题．

练习册系列答案

6．过点P（1，5）且与圆x²+y²-2x-4y-4=0相切的直线方程．

9．已知f（x）=lnx-x²+x+2，g（x）=x³-（1+2e）x²+（m+1）x+2，（m∈R），讨论f（x）与g（x）交点的个数．

16．已知函数f（x）=e${\;}^{\frac{{x}^{2}}{a}}$-ax有且只有一个零点，则实数a的取值范围为（-∞，0）∪{$\root{3}{2e}$}．

6．过原点的直线l与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右两支分别相交于A，B两点，F（-$\sqrt{3}$，0）是双曲线C的左焦点，若|FA|+|FB|=4，$\overrightarrow{FA}$$•\overrightarrow{FB}$=0．则双曲线C的方程=$\frac{{x}^{2}}{2}-{y}^{2}=1$．

13．

如图所示，在四棱锥中A-BCDE中，AE⊥面EBCD，且四边形EBCD是菱形，∠BED=120°，AE=BE=2，F是BC上的动点（不包括端点）．
（1）当F是BC的中点时，求点F到面ACD的距离；
（2）当F在由B向C移动的过程中，能否存在一个位置使得二面角F-AD-C的余弦值为$\frac{15}{\sqrt{231}}$？若存在，求出BF的长，若不存在，请说明理由．

10．

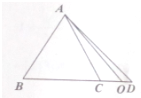如图，在△ABC中，点D是BC延长线上的点，$\overline{BC}$=3$\overline{CD}$，O在线段CD上且不与端点重合，若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+（1-x）$\overrightarrow{AC}$，则x的取值范围是（$-\frac{1}{3}$，0）．

11．已知函数f（x）=2sin（2x+φ）（|φ|＜$\frac{π}{2}）$的图象过点$（0，\sqrt{3}）$，则f（x）的图象的一个对称中心是（　　）

试题分类