题目内容
13. 如图所示,在四棱锥中A-BCDE中,AE⊥面EBCD,且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点(不包括端点).
如图所示,在四棱锥中A-BCDE中,AE⊥面EBCD,且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点(不包括端点).(1)当F是BC的中点时,求点F到面ACD的距离;
(2)当F在由B向C移动的过程中,能否存在一个位置使得二面角F-AD-C的余弦值为$\frac{15}{\sqrt{231}}$?若存在,求出BF的长,若不存在,请说明理由.
分析 (1)以E为原点,ED为y轴,EA为z轴,建立空间直角坐标系,求出平面ACD的法向量,由此能求出点F到面ACD的距离;
(2)设F($\sqrt{3}$,m,0),求出平面AFD的法向量,利用向量的夹角公式,即可得出结论.
解答  解:(1)以E为原点,ED为y轴,EA为z轴.
解:(1)以E为原点,ED为y轴,EA为z轴.
建立空间直角坐标系,由已知得F($\sqrt{3}$,0,0),A(0,0,2),C($\sqrt{3}$,1,0),D(0,2,0),
$\overrightarrow{AC}$=($\sqrt{3}$,1,-2),$\overrightarrow{AD}$=(0,2,-2),
设平面ACD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\sqrt{3}x+y-2z=0}\\{2y-2z=0}\end{array}\right.$,
取y=1,得$\overrightarrow{n}$=($\frac{\sqrt{3}}{3}$,1,1),
$\overrightarrow{AF}$=($\sqrt{3}$,0,-2),
∴点F到面ACD的距离d=$\frac{|\overrightarrow{AF}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{\sqrt{21}}{7}$.
(2)设F($\sqrt{3}$,m,0),平面AFD的法向量$\overrightarrow{m}$=(a,b,c),则
∵$\overrightarrow{AF}$=($\sqrt{3}$,m,-2),$\overrightarrow{AD}$=(0,2,-2),
∴$\left\{\begin{array}{l}{\sqrt{3}x+my-2=0}\\{2y-2z=0}\end{array}\right.$,
取y=1,得$\overrightarrow{m}$=($\frac{\sqrt{3}}{3}$(2-m),1,1),
∵二面角F-AD-C的余弦值为$\frac{15}{\sqrt{231}}$,
∴$\frac{|2-m+1+1|}{\sqrt{\frac{(2-m)^{2}}{3}+1+1}•\sqrt{\frac{1}{3}+1+1}}$=$\frac{15}{\sqrt{231}}$,
∴7m2-6m+187=0,方程无解,
∴不存在一个位置使得二面角F-AD-C的余弦值为$\frac{15}{\sqrt{231}}$.
点评 本题考查点到平面的距离的求法,考查二面角F-AD-C的余弦值,是中档题,正确求出平面的法向量是解题的关键.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
| A. | 30 | B. | 45 | C. | 63 | D. | 84 |
| 排队人数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
 如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点
如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点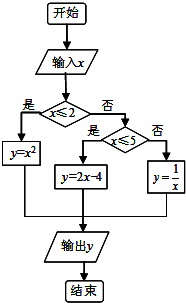 如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3.
如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3.