题目内容

6．过点P（1，5）且与圆x2+y2-2x-4y-4=0相切的直线方程．

分析 先求出圆的标准方程，可得圆心坐标和半径，P（1，5）满足圆的方程，从而得到答案．

解答 解：圆：x2+y2-2x-4y-4=0，即（x-1）2+（y-2）2=9，表示以C（1，2）为圆心，半径等于3的圆．
P（1，5）满足圆的方程，所以过点P（1，5）且与圆x2+y2-2x-4y-4=0相切的直线方程为y=5．

点评 本题主要考查圆的标准方程，考查学生的计算能力，属于基础题．

练习册系列答案
相关题目
16．在边长为2的等边△ABC中，点D满足$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$，点E满足$\overrightarrow{AE}$=λ$\overrightarrow{AC}$，λ∈[0，1]，则$\overrightarrow{EB}$•$\overrightarrow{ED}$的取值范围为[$\frac{23}{16}$，3]．
17．已知椭圆的焦点分别为F1（-4，0），F2（4，0），离心率e=0.8．
（1）求椭圆的标准方程；
（2）在椭圆上是否存在点P，使$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=0，若存在，求出坐标．
14．已知函数f（x）=ex-ax（e为自然对数的底数）．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）定义：函数F（x）的定义域为D，若?x0∈D，使F（x0）=x0成立，则称x0为F（x）的不动点．
当a=1时，
（ⅰ）证明：函数y=$\frac{1}{f（x）}$（x＞0）存在唯一的不动点x0，且x0∈（ln2，1）；
（ⅱ）已知数列{an}满足a1=ln2，an+1=$\frac{1}{f（{a}_{n}）}$（n∈N*），求证：?n∈N*，$\frac{f（{a}_{2n}）-f（{x}_{0}）}{{a}_{2n}-{x}_{0}}$＞f（x0）+x0-1，（其中x0为y=$\frac{1}{f（x）}$（x＞0）的不动点）．
1．已知x，y∈R，i为虚数单位，若$\frac{x}{1+i}$=1-yi，则x+yi=（　　）
A．2+iB．1+2iC．1-2iD．2-i
11．已知定义在R上的单调函数f（x）满足：对任意的x，都有f（f（x）-2x）=6，则不等式f（x+2）≥3f（-x）的解集为（　　）
A．[log2$\frac{3}{2}$，+∞）B．（-∞，log2$\frac{3}{2}$]C．[log25，+∞）D．（-∞，log25]
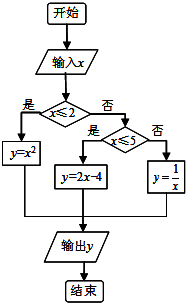4．确定函数y=${x}^{\frac{1}{3}}$$（1-x）^{\frac{2}{3}}$的单调区间，并求出此函数的极值．
1．在平面直角坐标系中，设向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），则$\overrightarrow{a}$．（$\overrightarrow{a}$-$\overrightarrow{b}$）=4．
2．如图给出了一个程序框图，其作用是输入x的值输出相应的y值，若要使输入的x值与输出的y值相等，则这样的x值的个数是3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网