题目内容
10.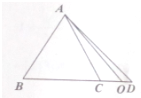 如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).
如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).
分析 结合图形,根据向量加法,$\overrightarrow{AO}=\overrightarrow{AC}+\overrightarrow{CO}$,可以想着用$\overrightarrow{AB},\overrightarrow{AC}$来表示$\overrightarrow{AO}$,根据已知条件知$\overrightarrow{CO}=k\overrightarrow{CD}=\frac{k}{3}(\overrightarrow{AC}-\overrightarrow{AB})$,其中0<k<1,从而便可得到$\overrightarrow{AO}=-\frac{k}{3}\overrightarrow{AB}+(1+\frac{k}{3})\overrightarrow{AC}$,从而x=$-\frac{k}{3}$,从而根据k的范围即可求出x的范围.
解答 解:$\overrightarrow{AO}=\overrightarrow{AC}+\overrightarrow{CO}$;
O在线段CD上且不与端点重合;
∴存在k,0<k<1,使$\overrightarrow{CO}=k\overrightarrow{CD}$;
又$\overrightarrow{BC}=3\overrightarrow{CD}$;
∴$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{BC}=\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})$;
∴$\overrightarrow{AO}=\overrightarrow{AC}+\frac{k}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$-\frac{k}{3}\overrightarrow{AB}+(1+\frac{k}{3})\overrightarrow{AC}$;
又$\overrightarrow{AO}=x\overrightarrow{AB}+(1-x)\overrightarrow{AC}$;
∴$x=-\frac{k}{3}$;
∴$-\frac{1}{3}<x<0$;
∴x的取值范围是$(-\frac{1}{3},0)$.
故答案为:($-\frac{1}{3}$,0).
点评 考查向量加法、减法的几何意义,共线向量基本定理,向量数乘的运算.

| A. | 30 | B. | 45 | C. | 63 | D. | 84 |
| A. | 3x+2y-21=0 | B. | 2x-3y-1=0 | C. | 3x-2y-9=0 | D. | 2x-3y+9=0 |
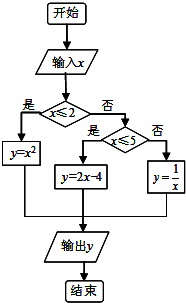 如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3.
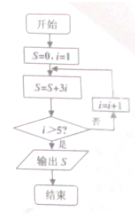
如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3. 已知MOD函数是一个求余数的函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入n=25时,则输出的结果为( )
已知MOD函数是一个求余数的函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入n=25时,则输出的结果为( )