题目内容
13. 如图,AB是半圆O的直径,P在AB的延长线上,PD与半圆O相切于点C,AD⊥PD.若PC=4,PB=2,则圆O的半径为3,CD=$\frac{12}{5}$.
如图,AB是半圆O的直径,P在AB的延长线上,PD与半圆O相切于点C,AD⊥PD.若PC=4,PB=2,则圆O的半径为3,CD=$\frac{12}{5}$.
分析 由PD与半圆O相切于点C及切割线定理得PC2=PB•PA,OC⊥PD.再利用AD⊥PD得到OC∥AD.利用平行线分线段成比例即可得出.
解答 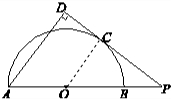 解:设圆的半径为R.连接OC.
解:设圆的半径为R.连接OC.
∵PD与半圆O相切于点C,∴PC2=PB•PA,OC⊥PD..
∵PC=4,PB=2,
∴42=2×(2+2R),
解得R=3.
又∵AD⊥PD,∴OC∥AD.
∴$\frac{PC}{CD}=\frac{PO}{OA}$.
∴$\frac{4}{CD}=\frac{2+3}{3}$,解得CD=$\frac{12}{5}$.
故答案为:3;$\frac{12}{5}$.
点评 熟练掌握圆的切线的性质、切割线定理、平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
4.已知函数f(x)=sin($\frac{k}{10}x+\frac{π}{3}$)(k≠0),当自变量x在任意两个整数之间(包括整数本身)变化时,至少包含一个周期,则最小正整数k是( )
| A. | 60 | B. | 61 | C. | 62 | D. | 63 |
1.已知数列{an}满足a1=2,nan+(n+1)an-1=0,x∈N*,且n≥2,则数列{$\frac{{a}_{n}}{(2n+1)(2n+3)}$}的前10项和为( )
| A. | $\frac{5}{69}$ | B. | $\frac{10}{69}$ | C. | $\frac{20}{69}$ | D. | $\frac{25}{69}$ |
8.在平面直角坐标系中,O为原点,A(-4,0)、B(0,4)、C(1,0),动点D满足|$\overrightarrow{CD}$|=1,则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最大值为( )
| A. | $\sqrt{29}$ | B. | 4$\sqrt{2}$ | C. | 6 | D. | 5 |
18.若向量$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(-1,1),$\overrightarrow{c}$=(4,2)满足(k$\overrightarrow{a}$+$\overrightarrow{b}$)∥$\overrightarrow{c}$,则k=( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |