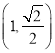题目内容
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,满足![]() .
.
(1)求角C的大小;
(2)设函数f(x)=cos(2x+C),将f(x)的图象向右平移![]() 个单位长度后得到函数g(x)的图象,求函数g(x)在区间
个单位长度后得到函数g(x)的图象,求函数g(x)在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() ;(2)
;(2)![]() 在
在![]() 时,最大值为1
时,最大值为1
【解析】试题分析:(1)根据![]() 由正弦定理及两角和与差角的三角函数可得
由正弦定理及两角和与差角的三角函数可得![]() ,可得
,可得![]() 的值;(2)由函数图象变换可得
的值;(2)由函数图象变换可得![]() ,由
,由![]() 求出
求出![]() ,和三角函数的有界性可得结果.
,和三角函数的有界性可得结果.
试题解析:(1)∵a,b,c是△ABC的内角A,B,C所对的三边,且![]() =
=![]() ,
,
∴由正弦定理得![]() =
=![]() ,
,
即(![]() sin A-sin B)cos C=cos Bsin C,
sin A-sin B)cos C=cos Bsin C,
即![]() sin Acos C=sin Bcos C+cos Bsin C=sin(B+C).
sin Acos C=sin Bcos C+cos Bsin C=sin(B+C).
∵A+B+C=π,∴sin(B+C)=sin A≠0,∴![]() cos C=1,即cos C=
cos C=1,即cos C=![]() .
.
∵C是△ABC的内角,∴C=![]() .
.
(2)由(1)可知f(x)=cos![]() ,g(x)=f
,g(x)=f![]() =cos
=cos![]() =cos(2x-
=cos(2x-![]() ).
).
∵0≤x≤![]() ,∴-
,∴-![]() ≤2x-
≤2x-![]() ≤
≤![]() ,∴g(x)在
,∴g(x)在![]() 时,最大值为1
时,最大值为1

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目