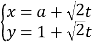题目内容
【题目】十九大提出,加快水污染防治,建设美丽中国![]() 根据环保部门对某河流的每年污水排放量
根据环保部门对某河流的每年污水排放量![]() 单位:吨
单位:吨![]() 的历史统计数据,得到如下频率分布表:
的历史统计数据,得到如下频率分布表:
污水量 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(Ⅰ)求在未来3年里,至1年污水排放量![]() 的概率;
的概率;
(Ⅱ)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元
时,经济损失为60万元![]() 为减少损失,现有三种应对方案:
为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费![]() 万元;
万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种方案,哪种方案好,并请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)采取方案二最好,理由详见解析.
;(Ⅱ)采取方案二最好,理由详见解析.
【解析】
(Ⅰ)先求污水排放量![]() 的概率0.25,然后再求未来3年里,至多1年污水排放量
的概率0.25,然后再求未来3年里,至多1年污水排放量![]() 的概率;
的概率;
(Ⅱ)分别求解三种方案的经济损失的平均费用,根据费用多少作出决策.
解:![]() Ⅰ
Ⅰ![]() 由题得
由题得![]() ,
,
设在未来3年里,河流的污水排放量![]() 的年数为Y,则
的年数为Y,则![]()
设事件“在未来3年里,至多有一年污水排放量![]() ”为事件A,
”为事件A,
则![]() .
.
![]() 在未来3年里,至多1年污水排放量
在未来3年里,至多1年污水排放量![]() 的概率为
的概率为![]() .
.
![]() Ⅱ
Ⅱ![]() 方案二好,理由如下:
方案二好,理由如下:
由题得![]() ,
,
![]() .
.
用![]() ,
,![]() ,
,![]() 分别表示方案一、方案二、方案三的经济损失,则
分别表示方案一、方案二、方案三的经济损失,则![]() 万元.
万元.
![]() 的分布列为:
的分布列为:
| 2 | 62 |
P |
|
|
![]() .
.
![]() 的分布列为:
的分布列为:
| 0 | 10 | 60 |
P |
|
|
|
![]() .
.
![]() 三种方案中方案二的平均损失最小,
三种方案中方案二的平均损失最小,![]() 采取方案二最好.
采取方案二最好.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
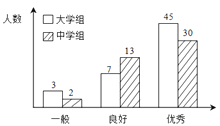
若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95﹪的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注: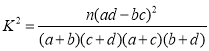 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.005 |
| 2.706 | 3.841 | 7.879 |
(2)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;