题目内容
【题目】某地拟建立一个艺术博物馆，采取竞标的方式从多家建筑公司选取一家建筑公经过层层筛选，甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家计了一个招标方案：两家公司从6个招标问题中随机抛取3个问题，已知这6个问中，甲公司可正确回答其中的4道题，而乙公司能正确回答每道题目的概率均为
，且甲、乙两家公司对每题的回答都是相互独立，互不影响的.
（I）求甲、乙两家公司共答对2道题的概率；
（II）设X为乙公司正确回答的题数，求随机变量X的分布列和数学期望.
【答案】(1)
;(2)见解析.
【解析】分析：（I）根据互斥事件的概率公式、独立事件概率公式，结合组合知识利用古典概型概率公式可得出两家公司答对
题的概率；(II)根据独立重复试验公式概率公式计算随机变量的概率，从而可得
的分布列，利用二项分布的期望公式可得的数学期望.
详解： （I）由题意可知，所求概率：
（II）乙公司正确回答的题数X的所有可能取值为0，1，2，3
∴X得分布列为：
∵
∴
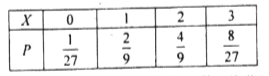
【题目】近年来，共享单车已经悄然进入了广大市民的日常生活，并慢慢改变了人们的出行方式.为了更好地服务民众，某共享单车公司在其官方
中设置了用户评价反馈系统，以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
条较为详细的评价信息进行统计，车辆状况的优惠活动评价的
列联表如下：
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
（1）能否在犯错误的概率不超过
的前提下认为优惠活动好评与车辆状况好评之间有关系？
（2）为了回馈用户，公司通过向用户随机派送每张面额为
元，元，
元的 三种骑行券.用户每次使用扫码用车后，都可获得一张骑行券.用户骑行一次获得
元券，获得元券的概率分别是
，
，且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车，记该用户当天获得的骑行券面额之和为
，求随机变量的分布列和数学期望.
参考数据：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：
，其中
.
【题目】十九大提出，加快水污染防治，建设美丽中国
根据环保部门对某河流的每年污水排放量
单位：吨
的历史统计数据，得到如下频率分布表：
污水量 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将污水排放量落入各组的频率作为概率，并假设每年该河流的污水排放量相互独立．
（Ⅰ）求在未来3年里，至1年污水排放量
的概率；
（Ⅱ）该河流的污水排放对沿河的经济影响如下：当
时，没有影响；当时，经济损失为10万元；当
时，经济损失为60万元为减少损失，现有三种应对方案：
方案一：防治350吨的污水排放，每年需要防治费
万元；
方案二：防治310吨的污水排放，每年需要防治费2万元；
方案三：不采取措施．
试比较上述三种方案，哪种方案好，并请说明理由．
