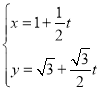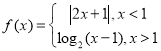题目内容
【题目】设常数![]() 在平面直角坐标系
在平面直角坐标系![]() 中,已知点
中,已知点![]() 直线
直线![]() 曲线
曲线![]() 与
与![]() 轴交于点A与
轴交于点A与![]() 交于点
交于点![]() 分别是曲线
分别是曲线![]() 与线段AB上的动点.
与线段AB上的动点.
(1)用![]() 表示点B到点F的距离;
表示点B到点F的距离;
(2)若![]() 且
且![]() 求
求![]() 的值;
的值;
(3)设![]() 且存在点P、Q,使得
且存在点P、Q,使得![]() 是等边三角形,求
是等边三角形,求![]() 的边长.
的边长.
【答案】(1)![]() (2)
(2)![]() (3)3
(3)3
【解析】
(1)运用平面内两点间距离公式求解;(2)由条件可知四边形AFPQ为正方形,转化为边长相等,即可得到m的解;(3)设出P,Q坐标利用|PF|=|FQ|求出t,即可求出两点坐标,进而求出边长.
解:(1)由 ,可得B(
,可得B(![]() ,m),
,m),
又F(0,![]() ),
),
∴|BF|![]() m﹣1,
m﹣1,
(2)由![]() 且
且![]() ,
,
则四边形AFPQ为正方形,
∵F(0,![]() ),A(0,m),P(1,
),A(0,m),P(1,![]() ),
),
∴|AF|=m![]() ,|FP|=1,
,|FP|=1,
∴m![]() 1,
1,
即m![]() 1,
1,
(3)由 可得B(
可得B(![]() ,2
,2![]() ),
),
设点Q(t,2![]() ),则||FQ|
),则||FQ|![]() ,(0≤t
,(0≤t![]() ),
),
设P(x0,y0),则|PF|![]() ,
,
∵△FPQ是等边三角形,
∴|PF|=|FQ|,即![]() ,即
,即![]() ,
,
代入曲线方程得 ,
,
∵|QF|2=|QP|2,t2+2=( )2+(
)2+(![]() )2,
)2,
解得t2=7,
|FQ|![]() 3
3
△FPQ的边长为3.


练习册系列答案
相关题目
【题目】为落实国家扶贫攻坚政策,某社区应上级扶贫办的要求,对本社区所有扶贫户每年年底进行收入统计,下表是该社区扶贫户中![]() 户从2016年至2019年的收入统计数据:(其中
户从2016年至2019年的收入统计数据:(其中![]() 为
为![]() 贫困户的人均年纯收人)
贫困户的人均年纯收人)
年份 | 2016年 | 2017年 | 2018年 | 2019年 |
年份代码 |
|
|
|
|
人均纯收入 |
|
|
|
|
(1)作出贫困![]() 户的人均年纯收人的散点图;
户的人均年纯收人的散点图;
(2)根据上表数据,用最小二乘法求出![]() 关于年份代码
关于年份代码![]() 的线性回归方程
的线性回归方程![]() ,并估计
,并估计![]() 贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于
贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于![]() 元)
元)
(参考公式: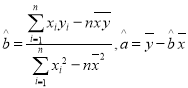 )
)